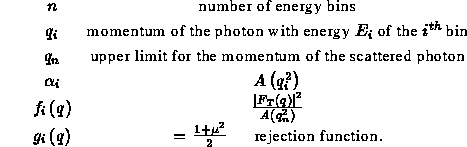Next: PHYS260 Cerenkov photons
Up: PHYS251 Simulation of
Previous: PHYS251 Simulation of
The Rayleigh differential cross section as a function of
is given
by []:
where:

Under the assumption that the atoms of a molecule are completely independent,
is given by:
where the index i runs on the N atoms in the molecule and:
|
|
|
|
|
|
|
|
|
|
|
|
Using the combined composition and rejection sampling method described in
GPAIRG ( [PHYS211]) we may set:
where:
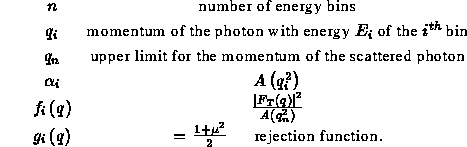
Therefore, for given values of the random numbers
and
, GRAYL
samples the momentum of the scattered photon and the scattering angle
via the following steps:
- sample
- find the
interval
which gives
- calculate the linear extrapolation:
- calculate
- calculate
- if
the event is accepted, otherwise
go back to 1.
F. Carminati
PHYS260
Janne Saarela
Mon Apr 3 12:46:29 METDST 1995