Sampling of the distribution function

The component distribution functions (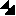) are given by

$f$r(0)(η)	$=$	$2e-\eta 2$	$=$	$2D$0(1,1,-η2)
$f$r(1)(η)			$=$	$2D$1(2,1,-η2)
$f$r(2)(η)			$=$	$D$2(3,1,-η2),

where $D$_n(a,b,z) = dⁿ[Γ(a)M(a,b,z)]/d aⁿ , with $M(a,b,z)$ the Kummers hypergeometric function.

Integrals of the functions $f$_r⁽¹⁾ and $f$_r⁽²⁾ needed for the Monte Carlo can be written down directly in terms of the D functions

$\int$η&inf;ηfr(1)&sp;ηdη	$=$	$D$1( 2,1, - η2)-D1( 1,1, - η2) - D0( 1,1,-η2)
$\int$η&inf;ηfr(2)&sp;ηdη	$=$	$\{12\}D$2(3,1,-η2) - D2(2,1,-η2) - D1(2,1,-η2)

We note that the first term is just the Gaussian part and it dominates for large B, that is, for large number of scatters, as it has to be expected. Recalling the definition of $\eta$ in (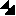) we can say that the half-width of the Gaussian part of the Molière distribution is $\sigma 2=\; \chi$_c²B/2 . Routine GMOLIE performs the sampling of the Molière distribution via the following steps:

1. the value of B is calculated recursively. If we set $f(B)\; =\; B$ with $f(B)\; =\; ln\Omega$₀+ lnB the relation used is $B$_n= B_n-1+ ΔB = B_n-1+ (f(B_n-1) - B_n-1)/(1-1/B_n-1) . Convergence is assumed when $|\Delta B|\; \le 10-4$ .

2. a random number $r$₁ is sampled and a table of four values $F$_r(η_i) is built with i = j-2,j-1,j,j+1 and $F$_r(η_j) ≥r₁ . F is the distribution function derived from ():

   $F$r(η)	$=$	$\int$0ηfr(t) &sp;dt= ∫0ηfr(0)(t)+fr(1)(t)B-1+fr(2)(t)B-2&sp;dt
   	$=$	$\int$0ηfr(0)(t) &sp;dt+ B-1∫0ηfr(1)(t) &sp;dt+B-2∫0ηfr(2)(t) &sp;dt
   	$=$	$F$r(0)(η) +B-1Fr(1)(η) + B-2Fr(2)(η)

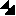   40 values of the functions $F$_r⁽ⁿ⁾ are tabulated.

3. using a four-points continued-fraction interpolation method (GMOL4) a table of $\eta$_i² is interpolated using the values of $r$₁ and F tabulated in the previous step. This is similar to the inversion of the distribution function, but instead of obtaining directly the random variable, we interpolate a table of its squares. This provides a better fit to the inverse function;

4. the value of $\theta =\; \chi$_cB η² is calculated;

5. a random number $r$₂ is extracted, and the rejection function $g(\theta )\; =sin\theta /\theta$ is computed. If $r$₂> g(θ)

   resampling begins from step 2, otherwise the value is accepted.

The Molière distribution gives the space scattering angle. A similar expression may be written for the lateral displacement of the scattered particles. However, the problem of joint angle lateral displacement in the Molière approximation has not been solved, and, for small step size, lateral displacement is of second order and may be neglected. This introduces a problem when large step sizes are taken. The step size can be artificially limited via the use of the variable STEMAX, which is an argument to the routine GSTMED. For more information on this point the user is invited to consult chapter [CONS200].