Restrictions on the step length

Restrictions on the length of the step arise from:

1. the number of scatters $\Omega$₀≥20 to stay within the multiple scattering regime. When $\Omega$₀< 20 , an appropriate number of single scatterings is used. See routine GMCOUL [PHYS328].
2. $\chi$_c²B ≤1 i.e. the width of the Gaussian part of the distribution should be less than one radian. This condition induces a maximum step length for the multiple scattering called $t$_Bethe . In order to find this value we write the limiting condition as $\chi$_c²(t_Bethe)B(t_Bethe) = 1 , that is $B(t$_Bethe) = 1/χ_c²(t_Bethe) . Now using equation (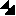) we take the exponential of both members $B(t$_Bethe) Ω₀(t_Bethe) = exp(1/χ_c²(t_Bethe)) . Dividing the two last equalities we obtain:

   $\Omega$0(tBethe) = {bcZinc2β2}tBethe	$=$	$\chi$c2(tBethe)exp(1/χc2(tBethe))
   	$=$	$\{\chi$cc2Zinc2tBetheexp[(E2β4)/(χcc2Zinc2tBethe)]E2β4}
   $exp[(E2\beta 4)/(\chi$cc2Zinc2tBethe)]	$=$	$\{b$cE2β2χcc2}
   $t$Bethe	$=$	$\{E2\beta 4\chi$cc2&sp;Zinc2&sp;ln[bcE2β2/χcc2]}

   For electrons and muons this constraint on the step-length is tabulated at initialisation time in the routine GMULOF [PHYS201]. For hadrons this formula can be approximated as:

   $t$_Gauss≈({114.1 &sp;10^-3}&sp;{E²βZ_inc})²X₀,

   where E is in GeV and $X$₀ is the radiation length in centimeters and the formula has been taken from the Gaussian approximation to multiple scattering (see [PHYS320]). This condition is more restrictive, because it is equivalent to require that the width of the Gaussian part of the distribution be less than $0.5$ , but it has been found that the two conditions are numerically equivalent;

3. limitation due to the path length correction algorithm used (see below).