Continuous energy loss

The integration of (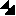) leads to the Berger-Seltzer formulae [,,,,,] :

$\{dEdx\}=\; \{2\; \pi r$₀²mn β²}[ln{2(τ+ 2)(I/m)²}+ F^±(τ, Δ)- δ],

where

The functions $F\pm$ are given by

$F+(\tau ,\Delta )$	$=$	$ln(\tau \Delta )\; -\{\Delta 2\tau \}[\tau +\; 2\; \Delta -\{3\Delta 2y2\}-(\Delta -\; \{\Delta 33\})\; y2-\; (\{\Delta 22\}-\; \tau \{\Delta 33\}+\; \{\Delta 44\})\; y3]$
$F-(\tau ,\Delta )$	$=$	$-1\; -\beta 2+ln[(\tau -\; \Delta )\Delta ]+\; \{\tau \tau -\Delta \}+\{[\{\Delta 22\}+\; (\; 2\tau +1)\; ln(1-\; \{\Delta \tau \})\; ]\gamma 2\},$

where $y\; =\; 1/(\gamma +1)$ .

The density effect correction is calculated as in []: $\delta =$

$0$	0
$2ln10\; +\; x+C+a(x$1-x)m	$if\; x$0≤x≤x1
$2ln10\; +\; x+C$	$if\; x$1<x,

$.$

where $x\; =\; ln(\gamma 2-1)\; /\; (2ln10)$

The quantities n, I and the parameters of the density effect correction ($x$₀, x₁, C, a, m ) are computed in the routine GPROBI, and we give the corresponding formulae here. The electron density of the medium, n, can be written as

$n\; =$

$N$Avρ{ZA}	$for\; elements$
$N$Avρ{∑iniZi∑iniAi}	$for\; compounds/mixtures,$

$.$

where

N

Avogadro's number;

$Z$_i

atomic number;

$A$_i

atomic weight;

$\rho$

density of the material;

$n$_i

proportion by number of the $ith$ element in the material (for a mixture $n$_i= W p_i/A_i

where $p$_i the proportion by weight and W is the molecular weight).

The average mean ionisation energy can be calculated as [] [] [] []:

$I\; (GeV)\; =$

$16\; 10-9\hspace{1em}Z0.9$	$for\; a\; chemical\; element$
$exp[\; \sum$iniZilnI(Zi) / ∑iniZ i]	$for\; a\; compound\; or\; mixture$

$.$

The density effect correction parameters can be computed (for condensed medium []) as

$C$	$=$	$1\; +\; 2ln\{I28.8\; 10-9\rho \sum \; n$iZi/ ∑ niAi}
$m$	$=$	$3$
$x$a	$=$	$\{C2ln10\}$
$a$	$=$	$2ln10\; \{(x$a-x0)(x1- x0)}m

$I$	$C$	$x$0	$x$1
		$0.2$	$2$
	$\ge 3.681$	$-0.326C-1$	$2$
$\ge 10-7$	$5.215$	$0.2$	$3$
$\ge 10-7$	$\ge 5.215$	$-0.326C-1.5$	$3$
$$