The cross-sections from [] have been used to calculate
data points for (![]() ) and (
) and (![]() ).
These have been parameterised as:
).
These have been parameterised as:
|
| |||
|
|
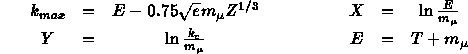
where is the maximum possible value of the photon energy. The functions ( ) are polynomials:
|
| ||
|
| ||
|
| ||
|
|
A least-squares fit has been performed on more than 2000 points for Z = 1, 6, 13, 26, 50, 82, 92 and 1 GeV 10 TeV and 10 keV . The resulting values of , , , , , and
can be found in the DATA statements within the functions
GBRSGM and GBRELM which
compute formulae (![]() ) and (
) and (![]() ) respectively.
) respectively.
The accuracy of the fit can be estimated as:
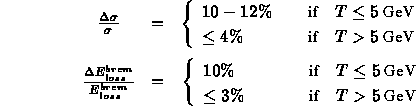
The contribution of the bremsstrahlung to the total energy loss of the muons is less than 1% for 5 GeV.
When
, a parameterisation different from
(![]() ) can be used for the total muon energy loss due to
bremsstrahlung:
) can be used for the total muon energy loss due to
bremsstrahlung:
|
| ||
|
| ||
|
|
where
.
The accuracy of the formula (![]() ) for
) for
is rather good:
|
| ||
|
|