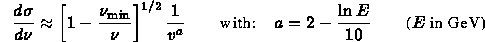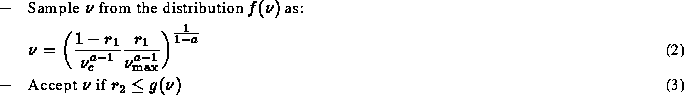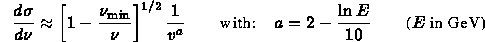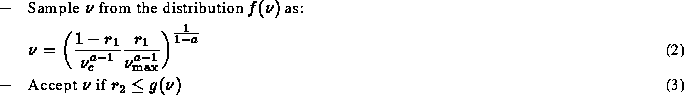Next: PHYS460 Muon-nucleus interactions
Up: PHYS451 Simulation of
Previous: Subroutines
The double differential cross-section for the
process can be written []:
|
|
|
|
All the quantities in the expression above are defined in [PHYS450].
By computing this cross-section for different
(
) points, it can be seen that:
-
the shape of the functions
and
practically does not depend on Z
-
the dominant contribution comes from the low
region:
-
in this low region (
)
is flat as a function of
Therefore, we propose the following sampling method as a rough approximation:
-
In the low
region the differential cross-section
can be approximated as:
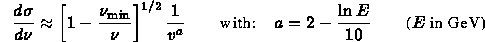
We can write:
where,
is the normalised distribution in the interval
and
is the rejection function.
-
and
being two uniformly distributed random numbers in the
interval
:
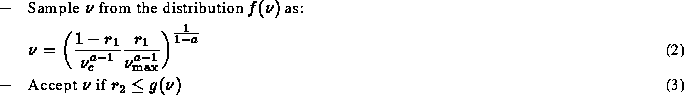
- Then compute
and generate
uniformly in the range
.
After the successful sampling of (
), GPAIRM generates the
polar
angles of the radiated -pair with respect to
an axis defined along the parent
muon's momentum.
is assigned the approximate average value:
is generated isotropically and
F. Carminati
PHYS460
Janne Saarela
Mon Apr 3 12:46:29 METDST 1995