GEOM050 The GEANT shapes

The GEANT geometry package offers sixteen basic shapes with which to describe the set.gif where particles are transported. In this section we will describe these shapes. For each shape figs (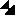), (), (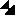), () 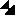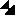show a simple drawing illustrating the meaning of the parameters and the position and orientation of the reference frame proper of that shape. A description of the shapes and of their parameters follows. Angles are always in degrees. With every shape is given the code which is used internally by GEANT to identify it.

1 BOX

box with faces perpendicular to the axes. It has 3 parameters:

1. DX half-length of the box along the x-axis;
2. DY half-length of the box along the y-axis;
3. DZ half-length of the box along the z-axis;

2 TRD1

trapezoid with the x dimension varying along z. It has 4 parameters:

1. DX1 half-length along x at the z surface positioned at -DZ;
2. DX2 half-length along x at the z surface positioned at +DZ;
3. DY half-length along the y-axis;
4. DZ half-length along the z-axis;

3 TRD2

trapezoid with both x and y dimensions varying along z. It has 5 parameters:

1. DX1 half-length along x at the z surface positioned at -DZ;
2. DX2 half-length along x at the z surface positioned at +DZ;
3. DY1 half-length along y at the z surface positioned at -DZ;
4. DY2 half-length along y at the z surface positioned at +DZ;
5. DZ half-length along the z-axis;

4 TRAP

general trapezoid: the faces perpendicular to z are trapezia and their centres are not necessarily on a line parallel to the z axis. This shape has 11 parameters, but only considering that the faces should be planar, only 9 are really independent. A check is performed on the user parameters and a message is printed in case of non-planar faces. Ignoring this warning may cause unpredictable effect at tracking time.

1. DZ half-length along the z axis;
2. THET polar angle of the line joining the centre of the face at -DZ to the centre of the one at +DZ;
3. PHI azimuthal angle of the line joining the centre of the face at -DZ to the centre of the one at +DZ;
4. H1 half-length along y of the face at -DZ;
5. BL1 half-length along x of the side at -H1 in y of the face at -DZ in z;
6. TL1 half-length along x of the side at +H1 in y of the face at -DZ in z;
7. ALP1 angle with respect to the y axis from the centre of the side at -H1 in y to the centre of the side at +H1 in y of the face at -DZ in z;
8. H2 half-length along y of the face at +DZ;
9. BL2 half-length along x of the side at -H2 in y of the face at +DZ in z;
10. TL2 half-length along x of the side at +H2 in y of the face at +DZ in z;
11. ALP2 angle with respect to the y axis from the centre of the side at -H2 in y to the centre of the side at +H2 in y of the face at +DZ in z;

5 TUBE

tube. It has 3 parameters:

1. RMIN inside radius;
2. RMAX outside radius;
3. DZ half length in z;

6 TUBS

$\phi$ segment of a tube. It has 5 parameters:

1. RMIN inside radius;
2. RMAX outside radius;
3. DZ half length in z;
4. PHI1 starting angle of the segment;
5. PHI2 ending angle of the segment;

PHI1 should be smaller than PHI2. If this is not the case, the system adds 360 degrees to PHI2.

7 CONE

conical tube. It has 5 parameters:

1. DZ half-length in z;
2. RMN1 inside radius at -DZ in z;
3. RMX1 outside radius at -DZ in z;
4. RMN2 inside radius at +DZ in z;
5. RMX2 outside radius at +DZ in z;

8 CONS

$\phi$ segment of a conical tube. It has 7 parameters:

1. DZ half-length in z;
2. RMN1 inside radius at -DZ in z;
3. RMX1 outside radius at -DZ in z;
4. RMN2 inside radius at +DZ in z;
5. RMX2 outside radius at +DZ in z;
6. PHI1 starting angle of the segment;
7. PHI2 ending angle of the segment;

PHI1 should be smaller than PHI2. If this is not the case, the system adds 360 degrees to PHI2.

9 SPHE

segment of spherical shell. It has 6 parameters:

1. RMIN inside radius of the shell;
2. RMAX outside radius of the shell;
3. THE1 starting polar angle of the shell;
4. THE2 ending polar angle of the shell;
5. PHI1 starting azimuthal angle of the shell;
6. PHI2 ending azimuthal angle of the shell;

10 PARA

parallelepiped. It has 6 parameters:

1. DX half-length in x;
2. DY half-length in y;
3. DZ half-length in z;
4. ALPH angle formed by the y axis and by the plane joining the centre of the faces parallel to the z-x plane at -DY and +DY;
5. THET polar angle of the line joining the centres of the faces at -DZ and +DZ in z;
6. PHI azimuthal angle of the line joining the centres of the faces at -DZ and +DZ in z;

11 PGON

polygon. It has at least 10 parameters:

1. PHI1 the azimuthal angle $\phi$ at which the volume begins (angles are counted counterclockwise);
2. DPHI opening angle of the volume, which extends from PHI1 to PHI1+DPHI;
3. NPDV number of sides of the cross section between the given $\phi$ limits;
4. NZ number of planes perpendicular to the z axis where the dimension of the section is given -- this number should be at least 2 and NP triplets of numbers must follow;
5. Z z coordinate of the section;
6. RMIN radius of the circle tangent to the sides of the inner polygon in the cross-section;
7. RMAX radius of the circle tangent to the sides of the outer polygon in the cross-section;

12 PCON

polycone. It has at least 9 parameters:

1. PHI1 the azimuthal angle $\phi$ at which the volume begins (angles are counted counterclockwise);
2. DPHI opening angle of the volume, which extends from PHI1 to PHI1+DPHI;
3. NZ number of planes perpendicular to the z axis where the dimension of the section is given -- this number should be at least 2 and NP triplets of numbers must follow;
4. Z z coordinate of the section;
5. RMIN radius of the inner circle in the cross-section;
6. RMAX radius of the outer circle in the cross-section;

13 ELTU

elliptical cross-section tube. It has three parameters:

1. P1 semi-axis of the ell.gife along x;
2. P2 semi-axis of the ell.gife along y;
3. DZ half-length in z;

The equation of the surface is $x2P1-2+\; y2P2-2=\; 1$ .

14 HYPE

hyperbolic tube, i.e. the inner and outer surfaces are hyperboloids, as would be formed by a system of cylindrical wires which were then rotated tangentially about their centres. It has 4 parameters:

1. RMIN inner radius at z=0, where tube is narrowest;
2. RMAX outer radius at z=0, where tube is narrowest;
3. DZ half-length in z;
4. THET stereo angle of rotation of the two faces;

The hyperbolic surfaces are given by: $r2=\; (z\; tan\theta )2+r$_z=0²

28 GTRA

general twisted trapezoid: the faces perpendicular to z are trapezia and their centres are not necessarily on a line parallel to the z axis as the TRAP; additionally, the faces may be twisted so that none of their edges are parallel. It is a TRAP shape, except that it is twisted in the x-y plane as a function of z. The parallel sides perpendicular to the z axis are rotated with respect to the x axis by an angle TWIST, which is one of the parameters. The shape is defined by the eight corners and is assumed to be constructed of straight lines joining points on the boundary of the trapezoidal face at z=-DZ to the corresponding points on the face at z=DZ. Divisions are not allowed. It has 12 parameters:

1. DZ half-length along the z axis;
2. THET polar angle of the line joining the centre of the face at -DZ to the centre of the one at +DZ;
3. PHI azimuthal angle of the line joining the centre of the face at -DZ to the centre of the one at +DZ;
4. TWIST twist angle of the faces parallel to the x-y plane at z = $\pm$ DZ around an axis parallel to z passing through their centre;
5. H1 half-length along y of the face at -DZ;
6. BL1 half-length along x of the side at -H1 in y of the face at -DZ in z;
7. TL1 half-length along x of the side at +H1 in y of the face at -DZ in z;
8. ALP1 angle with respect to the y axis from the centre of the side at -H1 in y to the centre of the side at +H1 in y of the face at -DZ in z;
9. H2 half-length along y of the face at +DZ;
10. BL2 half-length along x of the side at -H2 in y of the face at +DZ in z;
11. TL2 half-length along x of the side at +H2 in y of the face at +DZ in z;
12. ALP2 angle with respect to the y axis from the centre of the side at -H2 in y to the centre of the side at +H2 in y of the face at +DZ in z;

Note: this shape suffers from the same limitations than the TRAP: the tracking routines assume that the faces are planar, but this constraint is not easily expressed in terms of the 12 parameters. Additionally, no check on the faces is performed in this case. Users should avoid to use this shape as much as possible, and if they have to do so, they should make sure that the faces are really planes. If this is not the case, the result of the transport is unpredictable.

To accelerate the computations necessary for transport, 18 additional parameters are calculated for this shape:

1. DX0DZ $dx/dz$ of the line joining the centres of the faces at z=$\pm$ DZ;
2. DY0DZ $dy/dz$ of the line joining the centres of the faces at z=$\pm$ DZ;
3. X01 x at z=0 for line joining the + on parallel side, perpendicular corners at z=$\pm$ DZ;
4. Y01 y at z=0 for line joining the + on parallel side, + on perpendicular corners at z=$\pm$ DZ;
5. DXDZ1 $dx/dz$ for line joining the + on parallel side, + on perpendicular corners at z=$\pm$ DZ;
6. DYDZ1 $dy/dz$ for line joining the + on parallel side, + on perpendicular corners at z=$\pm$ DZ;
7. X02 x at z=0 for line joining the - on parallel side, + on perpendicular corners at z=$\pm$ DZ;
8. Y02 y at z=0 for line joining the - on parallel side, + on perpendicular corners at z=$\pm$ DZ;
9. DXDZ2 $dx/dz$ for line joining the - on parallel side, + on perpendicular corners at z=$\pm$ DZ;
10. DYDZ2 $dy/dz$ for line joining the - on parallel side, + on perpendicular corners at z=$\pm$ DZ;
11. X03 x at z=0 for line joining the - on parallel side, - on perpendicular corners at z=$\pm$ DZ;
12. Y03 y at z=0 for line joining the - on parallel side, - on perpendicular corners at z=$\pm$ DZ;
13. DXDZ3 $dx/dz$ for line joining the - on parallel side, - on perpendicular corners at z=$\pm$ DZ;
14. DYDZ3 $dy/dz$ for line joining the - on parallel side, - on perpendicular corners at z=$\pm$ DZ;
15. X04 x at z=0 for line joining the + on parallel side, - on perpendicular corners at z=$\pm$ DZ;
16. Y04 y at z=0 for line joining the + on parallel side, - on perpendicular corners at z=$\pm$ DZ;
17. DXDZ4 $dx/dz$ for line joining the + on parallel side, - on perpendicular corners at z=$\pm$ DZ;
18. DYDZ4 $dy/dz$ for line joining the + on parallel side, - on perpendicular corners at z=$\pm$ DZ;

29 CTUB

cut tube, a tube cut at the extremities with planes not necessarily perpendicular to the z axis. It has 11 parameters:

1. RMIN inside radius;
2. RMAX outside radius;
3. DZ half length in z;
4. PHI1 starting angle of the segment;
5. PHI2 ending angle of the segment;
6. LX x component of a unit vector perpendicular to the face at -DZ;
7. LY y component of a unit vector perpendicular to the face at -DZ;
8. LZ z component of a unit vector perpendicular to the face at -DZ;
9. HX x component of a unit vector perpendicular to the face at +DZ;
10. HY y component of a unit vector perpendicular to the face at +DZ;
11. HZ z component of a unit vector perpendicular to the face at +DZ;

PHI1 should be smaller than PHI2. If this is not the case, the system adds 360 degrees to PHI2.

Figure: shapes BOX, TRD1, TRD2, TRAP

Figure: shapes TUBE, TUBS, CONE, CONS

Figure: shapes PARA, SPHE, PGON, PCON

Figure: shapes GTRA

GEOM100