Continuous energy loss

The integration of () leads to the Bethe-Block stopping power or to the restricted energy loss formula []: $\{1\rho \}(\{dEdx\})\; =$

$D\; \{Z\; Z$inc2A β2}[ln( {2 meβ2γ2TmaxI2}) - 2 β2- δ-{ 2 CeZ}]	$if$	$T$cut≥Tmax
$D\; \{Z\; Z$inc2A β2}[ln( { 2 meβ2γ2TcI2}) - β2( 1 + {TcTmax}) - δ-{2 CeZ}]	$if$	$T$cut< Tmax

$.$

where,

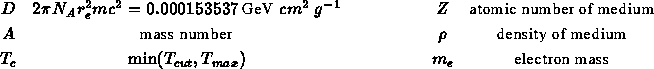
and I is the average ionisation potential of the atom in question. There exists a variety of phenomenological approximations for this. In former versions of GEANT the formula quoted by [] was used ( eV). At present the values recommended by [] are used. The ionisation potential I only enters into the logarithmic term of the energy loss formula, but it has been verified that the new parameterisation gives better accuracy especially in the case of high Z. It should be noted that this is not the value of I which is stored in the material data structure by GPROBI, which is still calculated as eV.

Note: the ionisation potential I must not be changed blindly, hoping that the most up-to-date values give the better results. The value of I is closely connected to the shell correction term (see later).

$\delta$ is a correction term which takes account of the reduction in energy loss due to the so-called density effect. This becomes important at high energy because media have a tendency to become polarised as the incident particle velocity increases. As a consequence, the atoms in a medium can no longer be considered as isolated. To correct for this effect the formulation of Sternheimer [,] is used:

$\delta =$

$0$	$if$	0
$4.606X\; +\; C\; +\; a(X$1-X)m	$if$	$X$0≤X < X1
$4.606X\; +\; C$	$if$	$X\; \ge X$1

$.$

where the medium-dependent constants are calculated as follows:

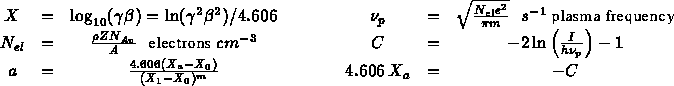
For condensed media we have:

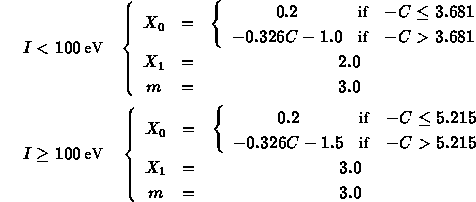
and in the case of gaseous media m=3 and:

$X$0= 1.6	$X$1= 4	$for$		$C$	$\le 9.5$
$X$0= 1.7	$X$1= 4	$for$		$C$	$\le 10$
$X$0= 1.8	$X$1= 4	$for$		$C$	$\le 10.5$
$X$0= 1.9	$X$1= 4	$for$		$C$	$\le 11$
$X$0= 2.	$X$1= 4	$for$		$C$	$\le 12.25$
$X$0= 2.	$X$1= 5	$for$		$C$	$\le 13.804$
$X$0= 0.326C-2.5	$X$1= 5	$for$		$C$

$C$_e/Z is a so-called shell correction term which accounts for the fact that, at low energies for light elements and at all energies for heavy ones, the probability of collision with the electrons of the inner atomic shells (K, L, etc.) is negligible. The semi-empirical formula used in GEANT, applicable to all materials, is due to Barkas []:

$C$e(I,η)	$=$	$(0.42237\eta -2+0.0304\eta -4-0.00038\eta -6)10-6I2$
	$+$	$(3.858\eta -2-0.1668\eta -4+0.00158\eta -6)10-9I3$
$\eta$	$=$	$\gamma \beta$

$C$_e is a dimensionless constant, but as I in the original article was expressed in eV and in GEANT it is expressed in GeV, the exponent of ten in the $I2$ -term is $10-6+2\; x9=\; 1012$ , and that of the $I3$ -term is $10-9+3\; x9=\; 1018$ .) This formula breaks down at low energies, and it only applies for values of $\eta >\; 0.13$ (i.e. $T\; >\; 7.9$ MeV for a proton). For $\eta \le 0.13$ the shell correction term is calculated as:

$.\; C$_e(I,η) 0mm5mm|_η≤0.13= C_e(I,η=0.13){ln( {TT_2l})ln( {7.9 &sp;10^-3&sp;GeVT_2l})}

i.e. the correction is switched off logarithmically from $T=7.9$

MeV to $T=T$_2l=2 MeV. GDRELX has been tested for protons against energy loss tables [,] for various materials in the energy range 50 MeV-25 GeV. Typical discrepancies are as follows:

Beryllium:	1.1at 0.05 GeV	0.02at 25 GeV
Hydrogen :	1.5at 0.05 GeV	12.1at 25 GeV
Water :	8.1at 0.05 GeV	4.4at 6 GeV

The mean energy loss can be described by the Bethe-Bloch formula () only if the projectile velocity is larger than that of orbital electrons. In the low-energy region where this is not verified, a different kind of parameterisation has been chosen []:

$\{1\rho \}\{dEdx\}=$

$I:$	$C$1τ{12}	$for$	$0\; \le T\; \le T$1l= 10 &sp;keV
$II:$	$\{S$LxSHSL- SH}	$for$	$T$1l< T ≤T2l= 2 &sp;MeV
$III:$	$Bethe-Bloch(\; 1+\{\nu T\})$	$for$	$T$2l< T

$.$

where

$S$L	$=$	$C$2τ0.45	$S$H	$=$	$\{C$3τ}ln[ 1+{C4τ}+C5τ]
$\tau$	$=$	$\{TM$p}	$M$p	$=$	$proton\; mass$

 

4c$\{dEdx\}$calculated- {dEdx}measured
experiment	A bib-REYN	B bib-GREE	C bib-SAKA
projectile	p	p	p
T (MeV)	0.03-0.6	0.4-1	55,65,73
material	$H$2 , He, $N$2 , $O$2 , Ne, Ar, Xe	Cu, Ge, Sn, Pb	Al, Ti, Cu, Sn, Pb
exp err ()	$\sim$ 3	$\sim$ 2.5	$\sim$ 0.7
tot $N○$ of pts	121	52	15
$N○$ of pts
with	94	50	8
	114	52	13
	119	52	14
	121	52	15

Table: Test of GDRELP with low energy protons.

The formula used in the region $T\; >\; T$_2l ensures the continuity of the energy loss function at $T\; =\; T$_2l when the Bethe-Bloch formula and the parameterisation meet. The parameter $\nu$ is chosen in such a way that:

$\{1\rho \}.\; \{dEdx\}$_II|_T=T2l={1ρ}. {dEdx}_III|_T=T2l

The routine GDRELP calculates the stopping power or restricted energy loss only for $T\; >\; T$_2l ; below this kinetic energy it gives the stopping power (i.e. total energy loss) irrespectively of the value of $T$_cut . This approximation does not introduce a serious source of error since, in the case of a proton, at $T=T$_2l the maximum energy transferable to the atomic electron is $T$_max≈4 keV, and the restricted loss should be calculated only if $T$_cut< T_max .

GDRELP has been tested against experimental data and energy loss tables. Some of the test results are summarised in tables , and .

 

4c1 keV $\le T\; \le$ 100 MeV,31 pts per element bib-ANZI
Z	element	mean (r.m.s.) deviation in	max (r.m.s.) deviation in
1	$H$2	0.4	1.1
6	O	0.5	1.6
13	Al	0.6	2.1
29	Cu	0.7	2.0
82	Pb	0.7	2.3

Table: Test of GDRELP against stopping power tables. Stated accuracy of the tables is $\sim 5$ for $T\; >\; 0.5$ MeV and $\sim 10$ for MeV

The energy lost due to the soft $\delta$ -rays is tabulated during initialisation as a function of the medium and of the energy by routine GDRELA

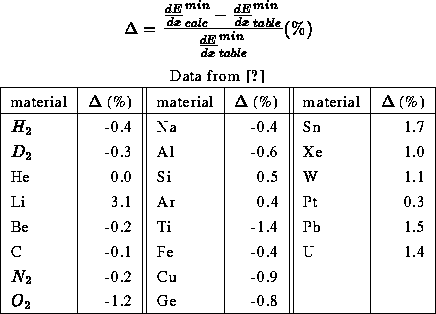
Table: The minimum stopping power calculated from the formula used is compared with values from the tables.

The tables are filled with the quantity $dE/dx$ in GeV $cm-1$

(formula () above). For a molecule or a mixture the following formula is used: $\{dEdx\}=\; \rho \sum$_ip_i( {dEdX})_i

where x is in cm, X in g $cm-2$ and $p$_i is the proportion by weight of the $Ith$ element.

The energy loss of all charged particles other than electrons, positrons and muons is obtained from that of protons by calculating the kinetic energy of a proton with the same $\beta$ , and using this value to interpolate the tables: $T$_proton={M_pM}T