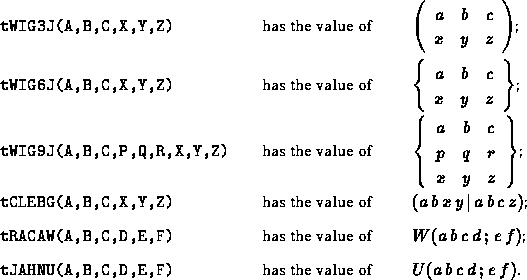
| Routine ID: U111 | |
|---|---|
| Author(s): K.S. Kölbig | Library: MATHLIB |
| Submitter: | Submitted: 15.10.1994 |
| Language: Fortran | Revised: |
Function subprograms RWIG3J, DWIG3J; RWIG6J, DWIG6J; RWIG9J, DWIG9J; RCLEBG, DCLEBG; RRACAW, DRACAW and RJAHNU, DJAHNU calculate the Wigner 3-j, 6-j and 9-j symbols, the Clebsch-Gordan coefficients, the Racah W-coefficients and the Jahn U-coefficients, respectively.
On CDC and Cray computers, the double-precision versions DWIG3J etc. are not available.
Structure:
FUNCTION subprograms
User Entry Names:
| RWIG3J, | RWIG6J, | RWIG9J, | RCLEBG, | RRACAW, | RJAHNU |
| DWIG3J, | DWIG6J, | DWIG9J, | DCLEBG, | DRACAW, | DJAHNU |
Usage:
In any arithmetic expression,
for
(type REAL), or
(type DOUBLE PRECISION),
All the arguments must have integral or half-integral values (see
Notes). They have the same type as the function name.
For definitions and notations see References.
The following relations hold (see Refs. 1 and 3):
Clebsch-Gordan coefficient (in terms of the Wigner 3-j symbol):
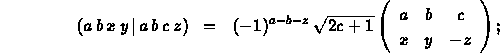
Racah W-coefficient (in terms of the Wigner 6-j symbol):
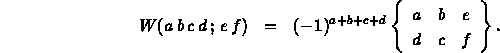
Jahn U-coefficient (in terms of the Wigner 6-j symbol and the Racah W-coefficient):
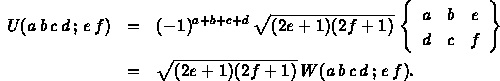
Method:
The Wigner 3-j symbol and the Clebsch-Gordan coefficient are calculated from formulas (5.1) and (5.10) of Ref. 1, respectively. The Wigner 6-j symbol, the Racah W- and the Jahn U-coefficient are calculated from formulas (5.23) and (5.24) of Ref. 1. In both cases, the factorials are replaced by their logarithms during the calculation. The Wigner 9-j symbol is calculated from formula (5.37) of Ref. 1 in terms of Wigner 6-j symbols.
Notes:
A Wigner-3j symbol
|
| ||
|
|
is considered to be zero unless simultaneously
| (i) | and have both either integral or half-integralvalues (each ), |
| (ii) | (each ), |
| (iii) | , |
| (iv) | is an integer, and |
| (v) | is an integer and . |
The conditions (v) are often denoted by and are called the triangle relations.
For a Clebsch-Gordan coefficient , condition (iii) reads and condition (iv) disappears.
A Wigner-6j symbol
|
| ||
|
|
is considered to be zero unless simultaneously
| (i) | all and have non-negative integral orhalf-integral values, |
| (ii) | the four triangle relations&quad; &quad;hold. |
A Wigner-9j symbol
|
| ||
|
| ||
|
|
is considered to be zero unless simultaneously
| (i) | all have non-negative integral or half-integralvalues, |
| (ii) | the arguments in each row and in each column satisfy thetriangle relations. |
Restrictions:
The sum of arguments in any triangle relation must not exceed 100. No test is made.
References: