U112 Clebsch-Gordan Coefficients in Rational Form

Function subprogram RTCLGN calculates the (signed) square of the Clebsch-Gordan coefficient in rational form and in powers of prime numbers. In terms of the Wigner-3j symbol, this coefficient is defined by

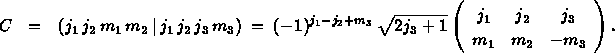
All $j$_i and $m$_i must have integral or half-integral values (see Notes). For definitions and notations see Ref. 1.

On computers other than CDC and Cray, only the double-precision version DTCLGN is available. On CDC and Cray computers, only the single-precision version RTCLGN is available.

Structure:

SUBROUTINE subprogram
User Entry Names: RTCLGN
Files Referenced: Unit 6

Usage:

For $t=R$ (type REAL), $t=D$ (type DOUBLE PRECISION),

    CALL tTCLGN(JJ1,JJ2,JJ3,MM1,MM2,MM3,RNUM,RDEN,KPEX)

JJ1,JJ2,JJ3

( INTEGER) The j-parameters multiplied by two, i.e. JJ1$=2j$₁ etc.

MM1,MM2,MM3

( INTEGER) The m-parameters multiplied by two, i.e. MM1$=2m$₁ etc.

RNUM

(type according to t) Contains, on exit, the signed numerator of $C2$ .

RDEN

(type according to t) Contains, on exit, the denominator of $C2$ .

KPEX

( INTEGER) Array of length 40 at least. Contains, on exit, the exponents $k$_n in the expression

$C2$

$=$

$$n=140pnkn,

where $p$₁=2, p₂=3, p₃=5,..., p₄₀=173 are the first 40 prime numbers.

Notes:

A Clebsch-Gordan coefficient $(j$₁ j₂ m₁ m₂ | j₁ j₂ j₃ m₃)

is considered to be zero unless simultaneously

(i)	$j$i and $m$i have both either integral or half-integralvalues (each $i$ ),
(ii)	$j$i≥|mi| ≥0 (each $i$ ),
(iii)	$m$1+m2=m3 ,
(iv)	$j$1+j2+j3 is an integer and $j$1+j2≥j3, &quad;j2+j3≥j1, &quad;j3+j1≥j2 .

In this case, $RNUM\; =\; 0$ , $RDEN\; =\; 1$ or $DNUM\; =\; 0$ , $DDEN\; =\; 1$ , respectively, and $KPEX(n)\; =\; 0,\hspace{0.17em}(n=1,...,40)$ .

This subroutine is based on an earlier version by H. Yoshiki.

Error handling:

Error U112.1: The calculation requires a prime number $p$_n with n>40.
In this case, $DNUM\; =\; 0$ , $DDEN\; =\; 1$ , $KPEX(n)\; =\; 0,\hspace{0.17em}(n=1,...,40)$ . A message is written on Unit 6 unless subroutine MTLSET (N002) has been called.

References:

1. R.D. Cowan, The theory of atomic structure and spectra, (Univ. of California Press, Berkeley CA 1981) 142--144

U501