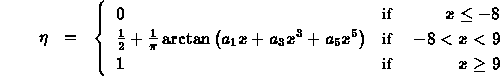
The radiative energy loss for electrons or positrons is:
|
| ||
|
|
Reference [] says that:
``The differences between the radiative loss of positrons
and electrons are considerable and cannot be disregarded.
[...] The ratio of the radiative energy loss for positrons to that for electrons obeys a simple scaling law, [...] is a function only of the quantity ''
In other words:
|
|
The authors have calculated this function in the range (here the kinetic energy T is expressed in MeV). Their data can be fairly accurately reproduced using a parametrisation:
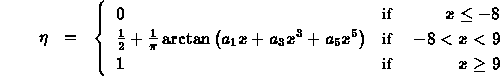
where:
|
| ||
|
| ||
|
| ||
|
| ||
|
|
This
energy loss difference is not a pure low-energy
phenomenon (at least for high Z), as it can be seen from
Tables ![]() ,
, ![]() and
and ![]() .
.
| 1c | 1c|T | 1c| | 1c
|
|
| |||
|
| |||
|
| |||
|
| |||
|
| |||
Table: ratio of the
radiative energy loss in lead
(Z=82).
The scaling holds for the ratio of the total radiative energy losses, but it is significantly broken for the photon spectrum in the screened case. In case of a point Coulomb charge the scaling would hold also for the spectrum. The scaling can be expressed by:
|
|
If we consider the photon spectrum from bremsstrahlung reported in [] we see that:
|
|
| 1cT(MeV) | 3|c|C | 3cPb | ||||
| &sp; |
| |||||
| 0.02 | -2.86 | -2.86 | +52.00 | -4.89 | -4.69 | +99.80 |
| 0.1 | -0.33 | -0.33 | +21.10 | -0.52 | -0.47 | +81.08 |
| 1 | +0.07 | +0.07 | +6.49 | +0.11 | +0.11 | +48.99 |
| 10 | 0.00 | 0.00 | +1.75 | 0.00 | +0.01 | +23.89 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | +9.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | +2.51 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | +0.00 | |
| 7c&sp; | ||||||
| 7c
&sp;and&sp;
|
Table: Difference in the energy loss and bremsstrahlung
cross-section for
in Carbon and Lead with a
cut for
and
of 10keV.
is
the value without the correction for the difference
.
We further assume that:
|
|
In order to satisfy approximately the scaling law for the ratio of the total radiative energy loss, we require for :
|
|
From the photon spectra we require:
We have chosen a simple function f:
|
|
| 1cT(MeV) | 3|c|C | 3cPb | ||||
| &sp; |
| |||||
| 2 | +4.19 | +4.21 | +7.29 | +4.47 | +6.88 | +61.78 |
| 10 | +0.87 | +0.87 | +1.93 | +0.87 | +1.14 | +26.29 |
| +0.08 | +0.08 | 0.00 | +0.06 | +0.06 | +9.10 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | +2.42 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | +0.00 | |
| 7c&sp; | ||||||
| 7c
&sp;and&sp;
|
Table: Difference in the energy loss and bremsstrahlung
cross-section for
in Carbon and Lead with a
cut for
and
of 1MeV.
is
the value without the correction for the difference
.
| 5c
| ||||
| 1cDepth | 2cC | 2|cPb | ||
| 1c|( units) | No diff | diff | No diff | diff |
| 0.5 | -11.7 | -13.0 | -0.8 | -3.9 |
| 1.0 | -5.3 | -4.9 | -1.0 | -4.1 |
| 1.5 | +7.3 | +8.0 | -1.4 | -3.5 |
| 2.0 | +7.1 | +5.3 | -0.7 | -0.0 |
| 2.5 | +4.9 | +4.3 | +1.7 | +3.6 |
| 3.0 | +4.8 | +4.1 | +1.1 | +4.3 |
| 3.5 | +3.3 | +2.7 | +2.7 | +3.1 |
| 4.0 | +3.6 | +5.3 | +2.9 | +3.0 |
| 4.5 | +1.7 | +2.8 | +0.5 | +2.3 |
| 5.0 | +3.4 | +3.5 | -1.9 | +1.8 |
Table: Difference in the shower development
for
in Carbon and Lead.
No diff refers to the
value without the correction for the difference
.
from the conditions (![]() ), (
), (![]() ) we get:
) we get:
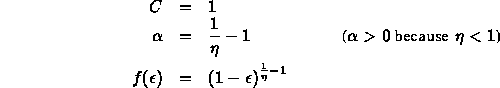
We have defined weight factors and for the positron continuous energy loss and discrete bremsstrahlung cross section:
|
|
where and is the photon cut BCUTE. In this scheme the positron energy loss and discrete bremsstrahlung can be calculated as:
|
|
As in this approximation the photon spectra are identical, the same SUBROUTINE is used for generating bremsstrahlung. The following relations hold:

which is consistent with the spectra.
The effect of this
bremsstrahlung difference can be also
seen in e.m. shower development, when the primary energy is not too
high. An example can be found in table ![]() .
.