//____________________________________________________________________
//  
/*

Principal Components Analysis (PCA)

The current implementation is based on the LINTRA package from CERNLIB by R. Brun, H. Hansroul, and J. Kubler. The class has been implemented by Christian Holm Cristensen in August 2000.

Introduction

In many applications of various fields of research, the treatment of large amounts of data requires powerful techniques capable of rapid data reduction and analysis. Usually, the quantities most conveniently measured by the experimentalist, are not necessarily the most significant for classification and analysis of the data. It is then useful to have a way of selecting an optimal set of variables necessary for the recognition process and reducing the dimensionality of the problem, resulting in an easier classification procedure.

This paper describes the implementation of one such method of feature selection, namely the principal components analysis. This multidimensional technique is well known in the field of pattern recognition and and its use in Particle Physics has been documented elsewhere (cf. H. Wind, Function Parameterization, CERN 72-21).

Overview

Suppose we have prototypes which are trajectories of particles, passing through a spectrometer. If one measures the passage of the particle at say 8 fixed planes, the trajectory is described by an 8-component vector:

$\begin{displaymath} \mathbf{x} = \left(x_1, x_2, \ldots, x_8\right) \end{displaymath}$

in 8-dimensional pattern space.

One proceeds by generating a a representative tracks sample and building up the covariance matrix $\mathsf{C}$ . Its eigenvectors and eigenvalues are computed by standard methods, and thus a new basis is obtained for the original 8-dimensional space the expansion of the prototypes,

$\begin{displaymath} \mathbf{x}_m = \sum^8_{i=1} a_{m_i} \mathbf{e}_i \quad \mbox{where} \quad a_{m_i} = \mathbf{x}^T\bullet\mathbf{e}_i \end{displaymath}$

allows the study of the behavior of the coefficients $a_{m_i}$ for all the tracks of the sample. The eigenvectors which are insignificant for the trajectory description in the expansion will have their corresponding coefficients $a_{m_i}$ close to zero for all the prototypes.

On one hand, a reduction of the dimensionality is then obtained by omitting these least significant vectors in the subsequent analysis.

On the other hand, in the analysis of real data, these least significant variables(?) can be used for the pattern recognition problem of extracting the valid combinations of coordinates describing a true trajectory from the set of all possible wrong combinations.

The program described here performs this principal components analysis on a sample of data provided by the user. It computes the covariance matrix, its eigenvalues ands corresponding eigenvectors and exhibits the behavior of the principal components ( $a_{m_i}$ ), thus providing to the user all the means of understanding his data.

A short outline of the method of Principal Components is given in subsection 1.3.

Principal Components Method

Let's consider a sample of prototypes each being characterized by variables $x_1, x_2, \ldots, x_P$ . Each prototype is a point, or a column vector, in a -dimensional pattern space.

$\begin{displaymath} \mathbf{x} = \left[\begin{array}{c} x_1\\ x_2\\ \vdots\\ x_P\end{array}\right]\,, \end{displaymath}$

(1)

where each

represents the particular value associated with the

-dimension.

Those variables are the quantities accessible to the experimentalist, but are not necessarily the most significant for the classification purpose.

The Principal Components Method consists of applying a linear transformation to the original variables. This transformation is described by an orthogonal matrix and is equivalent to a rotation of the original pattern space into a new set of coordinate vectors, which hopefully provide easier feature identification and dimensionality reduction.

Let's define the covariance matrix:

$\begin{displaymath} \mathsf{C} = \left\langle\mathbf{y}\mathbf{y}^T\right\rangl... ...athbf{y} = \mathbf{x} - \left\langle\mathbf{x}\right\rangle\,, \end{displaymath}$

(2)

and the brackets indicate mean value over the sample of

prototypes.

This matrix $\mathsf{C}$ is real, positive definite, symmetric, and will have all its eigenvalues greater then zero. It will now be show that among the family of all the complete orthonormal bases of the pattern space, the base formed by the eigenvectors of the covariance matrix and belonging to the largest eigenvalues, corresponds to the most significant features of the description of the original prototypes.

let the prototypes be expanded on into a set of basis vectors $\mathbf{e}_n, n=1,\ldots,N,N+1, \ldots, P$ ,

$\begin{displaymath} \mathbf{y}_i = \sum^N_{i=1} a_{i_n} \mathbf{e}_n, \quad i = 1, \ldots, M, \quad N < P \end{displaymath}$

(3)

The `best' feature coordinates $\mathbf{e}_n$ , spanning a feature space, will be obtained by minimizing the error due to this truncated expansion, i.e.,

$\begin{displaymath} \min\left(E_N\right) = \min\left[\left\langle\left(\mathb... ...\sum^N_{i=1} a_{i_n} \mathbf{e}_n\right)^2\right\rangle\right] \end{displaymath}$

(4)

with the conditions:

$\begin{displaymath} \mathbf{e}_k\bullet\mathbf{e}_j = \delta_{jk} = \left\{\b... ...for} & k = j\\ 0 & \mbox{for} & k \neq j \end{array}\right. \end{displaymath}$

(5)

Multiplying (3) by $\mathbf{e}^T_n$ using (5), we get

$\begin{displaymath} a_{i_n} = \mathbf{y}_i^T\bullet\mathbf{e}_n\,, \end{displaymath}$

(6)

so the error becomes

$\displaystyle E_N$	$\textstyle =$	$\displaystyle \left\langle\left[\sum_{n=N+1}^P a_{i_n}\mathbf{e}_n\right]^2\right\rangle$
	$\textstyle =$	$\displaystyle \left\langle\left[\sum_{n=N+1}^P \mathbf{y}_i^T\bullet\mathbf{e}_n\mathbf{e}_n\right]^2\right\rangle$
	$\textstyle =$	$\displaystyle \left\langle\sum_{n=N+1}^P \mathbf{e}_n^T\mathbf{y}_i\mathbf{y}_i^T\mathbf{e}_n\right\rangle$
	$\textstyle =$	$\displaystyle \sum_{n=N+1}^P \mathbf{e}_n^T\mathsf{C}\mathbf{e}_n$	(7)

The minimization of the sum in (7) is obtained when each term $\mathbf{e}_n^\mathsf{C}\mathbf{e}_n$ is minimum, since $\mathsf{C}$ is positive definite. By the method of Lagrange multipliers, and the condition (5), we get

$\begin{displaymath} E_N = \sum^P_{n=N+1} \left(\mathbf{e}_n^T\mathsf{C}\mathbf{e}_n - l_n\mathbf{e}_n^T\bullet\mathbf{e}_n + l_n\right) \end{displaymath}$

(8)

The minimum condition $\frac{dE_N}{d\mathbf{e}^T_n} = 0$ leads to the equation

$\begin{displaymath} \mathsf{C}\mathbf{e}_n = l_n\mathbf{e}_n\,, \end{displaymath}$

(9)

which shows that $\mathbf{e}_n$ is an eigenvector of the covariance matrix $\mathsf{C}$ with eigenvalue

. The estimated minimum error is then given by

$\begin{displaymath} E_N \sim \sum^P_{n=N+1} \mathbf{e}_n^T\bullet l_n\mathbf{e}_n = \sum^P_{n=N+1} l_n\,, \end{displaymath}$

(10)

where $l_n,\,n=N+1,\ldots,P$ are the eigenvalues associated with the omitted eigenvectors in the expansion (3). Thus, by choosing the

largest eigenvalues, and their associated eigenvectors, the error

is minimized.

The transformation matrix to go from the pattern space to the feature space consists of the ordered eigenvectors $\mathbf{e}_1,\ldots,\mathbf{e}_P$ for its columns

$\begin{displaymath} \mathsf{T} = \left[ \begin{array}{cccc} \mathbf{e}_1 & \... ...bf{e}_{2_P} & \cdots & \mathbf{e}_{P_P}\\ \end{array}\right] \end{displaymath}$

(11)

This is an orthogonal transformation, or rotation, of the pattern space and feature selection results in ignoring certain coordinates in the transformed space.

Christian Holm
August 2000, CERN

 
 */
//

// $Id: TPrincipal.cxx,v 1.10 2000/08/17 09:44:42 brun Exp $
// $Date: 2000/08/17 09:44:42 $
// $Author: brun $

#include "TPrincipal.h"

#include "TVectorD.h"
#include "TMatrixD.h"
#include "TList.h"
#include "TH2.h"
#include "TDatime.h"
#include "TBrowser.h"
#include "TROOT.h"

#include <fstream.h>
#include <iostream.h>
#include <iomanip.h>


ClassImp(TPrincipal); 

//____________________________________________________________________
 TPrincipal::TPrincipal() 
{
  // Empty CTOR, Do not use. 

      fHistograms = 0;
}

//____________________________________________________________________
 TPrincipal::TPrincipal(Int_t nVariables, Option_t *opt) 
  : fMeanValues(1,nVariables),
    fSigmas(1,nVariables),
    fCovarianceMatrix(1,nVariables, 1,nVariables),
    fEigenVectors(1,nVariables,1,nVariables),
    fEigenValues(1,nVariables),
    fOffDiagonal(1,nVariables),
    fUserData(nVariables*1000)
{
  // Ctor. Argument is number of variables in the sample of data 
  // Options are:
  //   N       Normalize the covariance matrix (default)
  //   <empty> Do not Normalize the covariance matrix
  //
  // The created object is  named "principal" and a reference to it
  // is added to the list of specials Root objects.
  // you can retrieve a pointer to the created object via:
  //  TPrincipal *principal = 
  //      (TPrincipal*)gROOT->GetListOfSpecials()->FindObject("principal");
  //
   if (nVariables <= 1) {
    Error("TPrincipal", "You can't be serious - nVariables == 1!!!");
    return;
  }

  //remove any previous object named "principal" in the list of special objects
  TObject *obj = gROOT->GetListOfSpecials()->FindObject("principal");
  if (obj) delete obj;
  SetName("principal");
  gROOT->GetListOfSpecials()->Add(this);
  
  fHistograms = 0;
  fIsNormalised       = kFALSE;
  fNumberOfDataPoints = 0;
  fNumberOfVariables  = nVariables; 
  while (strlen(opt) > 0) {
    switch(*opt++) {
    case 'N':
      fIsNormalised = kTRUE;
      break;
    default:
      break;
    }
  }

  if (!fMeanValues.IsValid())
    Error("TPrincipal","Couldn't create vector mean values");
  if (!fSigmas.IsValid())
    Error("TPrincipal","Couldn't create vector sigmas");
  if (!fCovarianceMatrix.IsValid())
    Error("TPrincipal","Couldn't create covariance matrix");
  if (!fEigenVectors.IsValid())
    Error("TPrincipal","Couldn't create eigenvector matrix");
  if (!fEigenValues.IsValid())
    Error("TPrincipal","Couldn't create eigenvalue vector");
  if (!fOffDiagonal.IsValid())
    Error("TPrincipal","Couldn't create offdiagonal vector");
  if (!fUserData.IsValid())
    Error("TPrincipal","Couldn't create user data vector");
}

//____________________________________________________________________
 TPrincipal::~TPrincipal() 
{
  // destructor

   gROOT->GetListOfSpecials()->Remove(this);
   
   if (fHistograms) {
      fHistograms->Delete();
      delete fHistograms;
   }
}

//____________________________________________________________________
 void TPrincipal::AddRow(Double_t *p) 
{
  // 
  /*

Add a data point and update the covariance matrix. The input array must be fNumberOfVariables long.

The Covariance matrix and mean values of the input data is caculated on the fly by the following equations:

$\begin{displaymath} \left<x_i\right>^{(1)} = x_{i1} \end{displaymath}$

$\begin{displaymath} \left<x_i\right>^{(n)} = \left<x_i\right>^{(n-1)} + \frac1n \left(x_{in} - \left<x_i\right>^{(n-1)}\right) \end{displaymath}$

$\begin{displaymath} C_{ij}^{(1)} = 0 \end{displaymath}$

$\begin{displaymath} C_{ij}^{(n)} = C_{ij}^{(n-1)} + \frac1{n-1}\left[\left(x_{i... ...\left<x_j\right>^{(n)}\right)\right] - \frac1n C_{ij}^{(n-1)} \end{displaymath}$

since this is a really fast method, with no rounding errors (please refer to CERN 72-21 pp. 54-106).

The data is stored internally in a TVectorD, in the following way:

$\begin{displaymath} \mathbf{x} = \left[\left(x_{11},\ldots,x_{P1}\right),\ldots, \left(x_{1i},\ldots,x_{Pi}\right), \ldots\right] \end{displaymath}$

With

as defined in the class description.

  */
  //  
  if (!p) 
    return; 

  // Increment the data point counter 
  Int_t i,j;
  if (++fNumberOfDataPoints == 1) {
    for (Int_t i = 0; i < fNumberOfVariables; i++)
      fMeanValues(i+1) = p[i];
  }
  else {
    
    Double_t cor = 1 - 1./Double_t(fNumberOfDataPoints - 1);
    for (i = 0; i < fNumberOfVariables; i++) {
      
      fMeanValues(i + 1) *= cor;
      fMeanValues(i + 1) += p[i] / Double_t(fNumberOfDataPoints - 1); 
      Double_t t1 = (p[i] - fMeanValues(i+1)) / (fNumberOfDataPoints - 1);
      
      // Setting Matrix (lower triangle) elements
      for (j = 0; j < i + 1; j++) {
	fCovarianceMatrix(i+1,j+1) *= cor;
	fCovarianceMatrix(i+1,j+1) += t1 * (p[j] - fMeanValues(j+1));  
      }
    }
  }
  
  // Store data point in internal vector
  // If the vector isn't big enough to hold the new data, then 
  // expand the vector by half it's size. 
  Int_t size = fUserData.GetNrows();
  if (fNumberOfDataPoints * fNumberOfVariables > size)
    fUserData.ResizeTo(size + size/2);
 
  for (i = 0; i < fNumberOfVariables; i++) {
     j = (fNumberOfDataPoints-1) * fNumberOfVariables + i;
    fUserData(j) = p[i];
  }
  
}

//____________________________________________________________________
 void TPrincipal::Browse(TBrowser *b)
{
  // Browse the TPrincipal object in the TBrowser. 
  if (fHistograms) {
    TIter next(fHistograms);
    TH1* h = 0;
    while ((h = (TH1*)next())) 
      b->Add(h,h->GetName());
  }
  
  b->Add(&fUserData,"User Data");
  b->Add(&fCovarianceMatrix,"Covariance Matrix");
  b->Add(&fMeanValues,"Mean value vector");
  b->Add(&fSigmas,"Sigma value vector");
  b->Add(&fEigenValues,"Eigenvalue vector");
  b->Add(&fEigenVectors,"Eigenvector Matrix");

}

//____________________________________________________________________
 void TPrincipal::Clear(Option_t *opt) 
{
  // Clear the data in Object. Notice, that's not possible to change
  // the dimension of the original data. 
  if (fHistograms) {
    fHistograms->Delete(opt);
  }
  
  fNumberOfDataPoints = 0;
  fTrace              = 0;
  fCovarianceMatrix.Zero();
  fEigenVectors.Zero();
  fEigenValues.Zero();
  fMeanValues.Zero();
  fSigmas.Zero();
  fOffDiagonal.Zero();
  
  fUserData.ResizeTo(fNumberOfVariables * 1000);
  fUserData.Zero();
}

//____________________________________________________________________
 const Double_t *TPrincipal::GetRow(Int_t row) 
{
  // Return a row of the user supplied data. 
  // If row is out of bounds, 0 is returned. 
  // It's up to the user to delete the returned array. 
  // Row 0 is the first row;
  if (row >= fNumberOfDataPoints) 
    return 0;
  
  Int_t index   = row  * fNumberOfVariables;
  return &fUserData(index);
}


//____________________________________________________________________
 void TPrincipal::MakeCode(const char *filename, Option_t *opt)
{
  // Generates the file <filename>, with .C appended if it does
  // argument doesn't end in .cxx or .C.
  //
  // The file contains the implementation of two functions
  //
  //    void X2P(Double_t *x, Double *p)
  //    void P2X(Double_t *p, Double *x, Int_t nTest)
  // 
  // which does the same as  TPrincipal::X2P and TPrincipal::P2X
  // respectively. Please refer to these methods.
  // 
  // Further, the static variables:
  //
  //    Int_t    gNVariables
  //    Double_t gEigenValues[]
  //    Double_t gEigenVectors[]
  //    Double_t gMeanValues[]
  //    Double_t gSigmaValues[]
  // 
  // are initialized. The only ROOT header file needed is Rtypes.h
  //
  // See TPrincipal::MakeRealCode for a list of options

  TString outName(filename);
  if (!outName.EndsWith(".C") && !outName.EndsWith(".cxx"))
    outName += ".C";

  MakeRealCode(outName.Data(),"",opt);
}

//____________________________________________________________________
 void TPrincipal::MakeEigenVectors() 
{
  // 
  /*

PRIVATE METHOD:
Find eigenvalues and vectors of tridiagonalised covariance matrix according to the QL with implicit shift algorithm from Numerical Recipes in C section 11.3.

The basic idea is to find matrices $\mathsf{Q}$ and $\mathsf{L}$ so that $\mathsf{C} = \mathsf{Q} \cdot \mathsf{L}$ , where $\mathsf{Q}$ is orthogonal and $\mathsf{L}$ is lower triangular. The QL algorithm consist of a sequence of orthogonal transformations

$\begin{displaymath} \mathsf{C}_s = \mathsf{Q}_s \cdot \mathsf{L}_s \end{displaymath}$

$\begin{displaymath} \mathsf{C}_{s+1} = \mathsf{L}_s \cdot \mathsf{Q}_s = \mathsf{Q}_s^T \cdot \mathsf{C}_s \cdot \mathsf{Q}_s \end{displaymath}$

(1) If $\mathsf{C}$ have eigenvalues with different absolute value $\vert l_i\vert$ , then $\mathsf{C}_s \rightarrow$ [lower triangular form] as $s\rightarrow\infty$ . The eigenvalues appear on the diagonal in increasing order of absolute magnitude. (2) If If $\mathsf{C}$ has an eigenvalue $\vert l_i\vert$ of multiplicty of order

, $\mathsf{C}_s \rightarrow$ [lower triangular form] as $s\rightarrow\infty$ , except for a diagona block matrix of order

, whose eigenvalues $\rightarrow l_i$ .

  */ 
  // 

  // See comments above on TPrincipal::MakeTridiagonal for more on
  // local changes. 

  TVectorD& d = fEigenValues;
  TVectorD& e = fOffDiagonal;
  TMatrixD& z = fEigenVectors;
  Int_t&    n = fNumberOfVariables;

  // It's convenient to renumber the e vector elements 
  for (Int_t i = 2; i <= n; i++) 
    e(i-1) = e(i);
  e(n) = 0;

  for (Int_t l = 1; l <= n; l++) {
    Int_t iter = 0;
    Int_t m    = 0;

    do {
      for (m = l; m <= n-1; m++) {
	// Look for a single small sub-diagonal element  to split the
	// matrix 
	Double_t dd = TMath::Abs(d(m)) + TMath::Abs(d(m+1));
	if ((Double_t)(TMath::Abs(e(m)) + dd) == dd)
	  break;
      }

      if (m != l) {
	if (iter++ == 30) {
	  Error("MakeEigenVectors","too many iterationsn");
	  return;
	}

	// Form shift
	Double_t g = (d(l+1) - d(l)) / (2 * e(l));
	Double_t r = TMath::Sqrt(g * g + 1);
	// This is d_m - k_s 
	g          = d(m) - d(l) + e(l) / (g + TMath::Sign(r,g));
	Double_t s = 1;
	Double_t c = 1;
	Double_t p = 0;
	Int_t i    = 0;
	for (i = m-1; i >= l; i--) {
	  // A plane rotation as in the original QL, followed by
	  // Givens rotations to restore tridiagonal form
          Double_t f = s * e(i); 
	  Double_t b = c * e(i);
	  r          = TMath::Sqrt(f*f + g*g);
	  e(i+1)     = r;

	  if (r == 0) {
	    // Recover from underflow
	    d(i + 1) -= p;
	    e(m)     =  0;
	    break;
	  }
	  s      = f / r;
	  c      = g / r;
	  g      = d(i+1) - p;
	  r      = (d(i) - g) * s + 2 * c * b;
	  p      = s * r;
	  d(i+1) = g + p;
	  g      = c * r - b;

	  for (Int_t k = 1; k <= n; k++) {
	    // Form Eigenvectors
	    f        = z(k,i+1);
	    z(k,i+1) = s * z(k,i) + c * f;
	    z(k,i)   = c * z(k,i) - s * f;
	  }
	}  // for (i = m)

	if (r == 0 && i >= l) 
	  continue;

	d(l) -= p;
	e(l)  = g;
	e(m)  = 0;
	
      } // if (m != l)
    } while (m != l);
  } // for (l = 0)
}

//____________________________________________________________________
 void TPrincipal::MakeHistograms(const char *name, Option_t *opt)
{
  // Make histograms of the result of the analysis. 
  // The option string say which histograms to create
  //      X         Histogram original data
  //      P         Histogram principal components corresponding to
  //                original data 
  //      D         Histogram the difference between the original data
  //                and the projection of principal unto a lower
  //                dimensional subspace (2D histograms)
  //      E         Histogram the eigenvalues
  //      S         Histogram the square of the residues 
  //                (see TPrincipal::SumOfSquareResidues)
  // The histograms will be named <name>_<type><number>, where <name>
  // is the first argument, <type> is one of X,P,D,E,S, and <number>
  // is the variable. 
  Bool_t makeX  = kFALSE;
  Bool_t makeD  = kFALSE;
  Bool_t makeP  = kFALSE;
  Bool_t makeE  = kFALSE;
  Bool_t makeS  = kFALSE;

  Int_t len     = strlen(opt);
  Int_t i,j,k;
  for (i = 0; i < len; i++) {
    switch (opt[i]) {
    case 'X':
    case 'x':
      makeX = kTRUE;
      break;
    case 'd':
    case 'D':
      makeD = kTRUE;
      break;
    case 'P':
    case 'p':
      makeP = kTRUE;
      break;
    case 'E':
    case 'e':
      makeE = kTRUE;
      break;
    case 's':
    case 'S':
      makeS = kTRUE;
      break;
    default:
      Warning("MakeHistograms","Unknown option: %c",opt[i]);
    }
  }

  // If no option was given, then exit gracefully
  if (!makeX && !makeD && !makeP && !makeE && !makeS)
    return;

  // If the list of histograms doesn't exist, create it. 
  if (!fHistograms) 
    fHistograms = new TList;

  // Don't create the histograms if they are already in the TList. 
  if (makeX && fHistograms->FindObject(Form("%s_x0",name))) 
    makeX = kFALSE;
  if (makeD && fHistograms->FindObject(Form("%s_d0",name))) 
    makeD = kFALSE;
  if (makeP && fHistograms->FindObject(Form("%s_p0",name))) 
    makeP = kFALSE;
  if (makeE && fHistograms->FindObject(Form("%s_e",name))) 
    makeE = kFALSE;
  if (makeS && fHistograms->FindObject(Form("%s_s",name))) 
    makeS = kFALSE;

  TH1F **hX  = 0;
  TH2F **hD  = 0;
  TH1F **hP  = 0;
  TH1F *hE   = 0;
  TH1F *hS   = 0;

  // Initialize the arrays of histograms needed 
  if (makeX)
    hX = new TH1F * [fNumberOfVariables]; 

  if (makeD)
    hD = new TH2F * [fNumberOfVariables]; 

  if (makeP)
    hP = new TH1F * [fNumberOfVariables]; 

  if (makeE){  
    hE = new TH1F(Form("%s_e",name), "Eigenvalues of Covariance matrix",
		  fNumberOfVariables,0,fNumberOfVariables);
    hE->SetXTitle("Eigenvalue");
    fHistograms->Add(hE);
  }
  
  if (makeS) {
    hS = new TH1F(Form("%s_s",name),"E_{N}",
		  fNumberOfVariables-1,1,fNumberOfVariables);
    hS->SetXTitle("N");
    hS->SetYTitle("#sum_{i=1}^{M} (x_{i} - x'_{N,i})^{2}");
    fHistograms->Add(hS);
  }
  
  // Initialize sub elements of the histogram arrays 
  for (i = 0; i < fNumberOfVariables; i++) {
    if (makeX) {
      // We allow 4 sigma spread in the original data in our
      // histogram. 
      Double_t xlowb  = fMeanValues(i+1) - 4 * fSigmas(i+1);
      Double_t xhighb = fMeanValues(i+1) + 4 * fSigmas(i+1);
      Int_t    xbins  = fNumberOfDataPoints/100;
      hX[i]           = new TH1F(Form("%s_x%d", name, i),
				 Form("Pattern space, variable %d", i),
				 xbins,xlowb,xhighb);
      hX[i]->SetXTitle(Form("x_{%d}",i));
      fHistograms->Add(hX[i]); 
    }
    
    if(makeD) {
      // The upper limit below is arbitrary!!!
      Double_t dlowb  = 0;
      Double_t dhighb = 20;
      Int_t    dbins  = fNumberOfDataPoints/100;
      hD[i]           = new TH2F(Form("%s_d%d", name, i),
				 Form("Distance from pattern to "
				      "feature space, variable %d", i),
				 dbins,dlowb,dhighb,
				 fNumberOfVariables-1,
				 1,
				 fNumberOfVariables);
      hD[i]->SetXTitle(Form("|x_{%d} - x'_{%d,N}|/#sigma_{%d}",i,i,i));
      hD[i]->SetYTitle("N");
      fHistograms->Add(hD[i]);
    }
    
    if(makeP) {
      // For some reason, the trace of the none-scaled matrix 
      // (see TPrincipal::MakeNormalised) should enter here. Taken
      // from LINTRA code. 
      Double_t plowb   = -10 * TMath::Sqrt(fEigenValues(i+1) * fTrace); 
      Double_t phighb  = -plowb;
      Int_t    pbins   = 100;
      hP[i]            = new TH1F(Form("%s_p%d", name, i),
				  Form("Feature space, variable %d", i),
				  pbins,plowb,phighb);
      hX[i]->SetXTitle(Form("p_{%d}",i));
      fHistograms->Add(hP[i]);
    }
    
    if (makeE)
      // The Eigenvector histogram is easy
      hE->Fill(i,fEigenValues(i+1));

  }
  for (i = 0; i < fNumberOfDataPoints; i++) {
    Double_t *x = 0;
    Double_t *p = new Double_t[fNumberOfVariables];
    Double_t *d = new Double_t[fNumberOfVariables];

    if (makeX||makeP||makeD||makeS)
      // update the original data histogram 
      x  = (Double_t*)(GetRow(i));

    if (makeP||makeD||makeS)
      // calculate the corresponding principal component
      X2P(x,p);

    if (makeD || makeS) {
      // Calculate the difference between the original data, and the
      // same project onto principal components, and then to a lower
      // dimensional sub-space
      for (j = fNumberOfVariables; j > 0; j--) {
	P2X(p,d,j);
      
	for (k = 0; k < fNumberOfVariables; k++) {
	  // We use the absolute value of the difference!
	  d[k] = x[k] - d[k];

	  if (makeS) 
	    hS->Fill(j,d[k]*d[k]);

	  if (makeD) {
	    d[k] = TMath::Abs(d[k]) / fSigmas(k+1);
	    (hD[k])->Fill(d[k],j);
	  }
	}
      }
    }
    
    if (makeX||makeP) {
      // If we are asked to make any of these histograms, we have to
      // go here
      for (j = 0; j < fNumberOfVariables; j++) {
	if (makeX)
	  (hX[j])->Fill(x[j]);      

	if (makeP)
	  (hP[j])->Fill(p[j]);
      }
    }
    
    // Clean up
    if (d)
      delete [] d;
    if (p)
      delete [] p;
  }

  // Normalize the residues
  if (makeS)
    hS->Scale(Double_t(1.)/fNumberOfDataPoints);
}

//____________________________________________________________________
 void TPrincipal::MakeNormalised() 
{
  // PRIVATE METHOD: Normalize the covariance matrix
  
  Int_t i,j;
  for (i = 1; i <= fNumberOfVariables; i++) {
    fSigmas(i) = TMath::Sqrt(fCovarianceMatrix(i,i));
    if (fIsNormalised) 
      for (j = 1; j <= i; j++) 
	fCovarianceMatrix(i,j) /= (fSigmas(i) * fSigmas(j));
    
    fTrace += fCovarianceMatrix(i,i);
  }

  // Fill remaining parts of matrix, and scale. 
  for (i = 1; i <= fNumberOfVariables; i++)     
    for (j = 1; j <= i; j++) {
      fCovarianceMatrix(i,j) /= fTrace;
      fCovarianceMatrix(j,i) = fCovarianceMatrix(i,j); 
    }

}

//____________________________________________________________________
 void TPrincipal::MakeMethods(const char *classname, Option_t *opt) 
{
  // Generate the file <classname>PCA.cxx which contains the
  // implementation of two methods:
  // 
  //    void <classname>::X2P(Double_t *x, Double *p)
  //    void <classname>::P2X(Double_t *p, Double *x, Int_t nTest)
  // 
  // which does the same as  TPrincipal::X2P and TPrincipal::P2X
  // respectivly. Please refer to these methods.
  // 
  // Further, the public static members:
  //
  //    Int_t    <classname>::fgNVariables
  //    Double_t <classname>::fgEigenValues[]
  //    Double_t <classname>::fgEigenVectors[]
  //    Double_t <classname>::fgMeanValues[]
  //    Double_t <classname>::fgSigmaValues[]
  // 
  // are initialized, and assumed to exist. The class declaration is
  // assumed to be in <classname>.h and assumed to be provided by the
  // user. 
  //
  // See TPrincipal::MakeRealCode for a list of options
  // 
  // The minimal class definition is:
  //
  //   class <classname> {
  //   public:
  //     static Int_t    fgNVariables;
  //     static Double_t fgEigenVectors[];
  //     static Double_t fgEigenValues[];
  //     static Double_t fgMeanValues[];
  //     static Double_t fgSigmaValues[];
  //     
  //     void X2P(Double_t *x, Double_t *p);
  //     void P2X(Double_t *p, Double_t *x, Int_t nTest);
  //   };
  // 
  // Whether the methods <classname>::X2P and <classname>::P2X should
  // be static or not, is up to the user. 

  
  MakeRealCode(Form("%sPCA.cxx", classname), classname, opt);
}


//____________________________________________________________________
 void TPrincipal::MakePrincipals() 
{
  // Perform the principal components analysis. 
  // This is done is several stages:
  // * Transform the covariance matrix into a tridiagonal matrix, using
  //   method Principal::MakeTridiagonal();
  // * Find the eigenvalues and vectors of the tridiagonal matrix,
  //   using the method Principal::MakeEigenVectors();
  
  // Normalize matrix
  MakeNormalised();

  // Tridiagonalize matrix
  MakeTridiagonal();

  // Make eigenvectors and -values
  MakeEigenVectors();

  // Order eigenvalues and -vectors
  MakeOrdered();
}

//____________________________________________________________________
 void TPrincipal::MakeOrdered()
{
  // 
  /*

PRIVATE METHOD:
Order the eigenvalues and vectors by ascending eigenvalue. The algorithm is a straight insertion. It's taken from Numerical Recipes in C section 11.1.

  */
  // 
    
    Int_t i,j,k;
    for (i = 1; i <= fNumberOfVariables; i++) {
       k = i;
    Double_t p = fEigenValues(i);

    for (j = i + 1; j <= fNumberOfVariables; j++)
      if (fEigenValues(j) >= p) {
	k = j;
	p = fEigenValues(j);
      }
    
    if (k != i) {
      fEigenValues(k) = fEigenValues(i);
      fEigenValues(i) = p;
      
      for (j = 1; j <= fNumberOfVariables; j++) {
	p                  = fEigenVectors(j,i);
	fEigenVectors(j,i) = fEigenVectors(j,k);
	fEigenVectors(j,k) = p;
      }
    }
  }   
}

//____________________________________________________________________
 void TPrincipal::MakeRealCode(const char *filename, const char *classname, Option_t *opt) 
{
  // PRIVATE METHOD:
  // This is the method that actually generates the code for the
  // transformations to and from feature space and pattern space 
  // It's called by TPrincipal::MakeCode and TPrincipal::MakeMethods. 
  //  
  // The options are: NONE so far

  Bool_t  isMethod = (classname[0] == '0' ? kFALSE : kTRUE);
  const char *prefix   = (isMethod ? Form("%s::", classname) : "");
  const char *cv_qual  = (isMethod ? "" : "static ");

  ofstream outFile(filename,ios::out|ios::trunc); 
  if (!outFile) {
    Error("MakeRealCode","couldn't open output file '%s'",filename); 
    return;
  }
  
  cout << "Writing on file "" << filename << "" ... " << flush;
  //
  // Write header of file 
  //
  // Emacs mode line ;-)
  outFile << "// -*- mode: c++ -*-" << endl;
  // Info about creator
  outFile << "// " << endl
	  << "// File " << filename
	  << " generated by TPrincipal::MakeCode" << endl;
  // Time stamp
  TDatime date;
  outFile << "// on " << date.AsString() << endl;
  // ROOT version info
  outFile << "// ROOT version " << gROOT->GetVersion() 
	  << endl << "//" << endl;
  // General information on the code
  outFile << "// This file contains the functions " << endl
	  << "//" << endl
	  << "//    void  " << prefix 
	  << "X2P(Double_t *x, Double_t *p); " << endl 
	  << "//    void  " << prefix 
	  << "P2X(Double_t *p, Double_t *x, Int_t nTest);" 
	  << endl << "//" << endl
	  << "// The first for transforming original data x in " << endl
	  << "// pattern space, to principal components p in " << endl
	  << "// feature space. The second function is for the" << endl
	  << "// inverse transformation, but using only nTest" << endl
	  << "// of the principal components in the expansion" << endl
	  << "// " << endl
	  << "// See TPrincipal class documentation for more "
	  << "information " << endl << "// " << endl;
  // Header files
  outFile << "#ifndef __CINT__" << endl;
  if (isMethod) 
    // If these are methods, we need the class header 
    outFile << "#include "" << classname << ".h"" << endl;
  else 
    // otherwise, we need the typedefs of Int_t and Double_t
    outFile << "#include <Rtypes.h> // needed for Double_t etc" << endl;
  // Finish the preprocessor block
  outFile << "#endif" << endl << endl;

  // 
  // Now for the data
  //
  // We make the Eigenvector matrix, Eigenvalue vector, Sigma vector,
  // and Mean value vector static, since all are needed in both
  // functions. Also ,the number of variables are stored in a static
  // variable. 
  outFile << "//" << endl 
	  << "// Static data variables"  << endl
	  << "//" << endl;
  outFile << cv_qual << "Int_t    " << prefix << "gNVariables = " 
	  << fNumberOfVariables << ";" << endl;

  // Assign the values to the Eigenvector matrix. The elements are
  // stored row-wise, that is element 
  //    M[i][j] = e[i * nVariables + j]
  // where i and j are zero-based.
  outFile << endl << "// Assignment of eigenvector matrix." << endl
	  << "// Elements are stored row-wise, that is" << endl
	  << "//    M[i][j] = e[i * nVariables + j] " << endl
	  << "// where i and j are zero-based" << endl;
  outFile << cv_qual << "Double_t " << prefix 
	  << "gEigenVectors[] = {" << flush;
  Int_t i,j;
  for (i = 0; i < fNumberOfVariables; i++) {
    for (j = 0; j < fNumberOfVariables; j++) {
      Int_t index = i * fNumberOfVariables + j;
      outFile << (index != 0 ? "," : "" ) << endl
	      << "  "  << fEigenVectors(i+1,j+1) << flush; 
    }
  }
  outFile << "};" << endl << endl;

  // Assignment to eigenvalue vector. Zero-based.
  outFile << "// Assignment to eigen value vector. Zero-based." << endl;
  outFile << cv_qual << "Double_t " << prefix 
	  << "gEigenValues[] = {" << flush;
  for (i = 0; i < fNumberOfVariables; i++) 
    outFile << (i != 0 ? "," : "") << endl
	    << "  " << fEigenValues(i+1) << flush;
  outFile << endl << "};" << endl << endl;

  // Assignment to mean Values vector. Zero-based.
  outFile << "// Assignment to mean value vector. Zero-based." << endl;
  outFile << cv_qual << "Double_t " << prefix 
	  << "gMeanValues[] = {" << flush;
  for (i = 0; i < fNumberOfVariables; i++) 
    outFile << (i != 0 ? "," : "") << endl
	    << "  " << fMeanValues(i+1) << flush;
  outFile << endl << "};" << endl << endl;

  // Assignment to mean Values vector. Zero-based.
  outFile << "// Assignment to sigma value vector. Zero-based." << endl;
  outFile << cv_qual << "Double_t " << prefix 
	  << "gSigmaValues[] = {" << flush;
  for (i = 0; i < fNumberOfVariables; i++) 
    outFile << (i != 0 ? "," : "") << endl
	    << "  " << fSigmas(i+1) << flush;
  outFile << endl << "};" << endl << endl;

  // 
  // Finally we reach the functions themselves
  // 
  // First: void x2p(Double_t *x, Double_t *p);
  //
  outFile << "// " << endl
	  << "// The " 
    	  << (isMethod ? "method " : "function ")
	  << "  void " << prefix 
	  << "X2P(Double_t *x, Double_t *p)" 
	  << endl << "// " << endl;
  outFile << "void " << prefix 
	  << "X2P(Double_t *x, Double_t *p) {" << endl
	  << "  for (Int_t i = 0; i < gNVariables; i++) {" << endl
	  << "    p[i] = 0;" << endl
	  << "    for (Int_t j = 0; j < gNVariables; j++)" << endl
	  << "      p[i] += (x[j] - gMeanValues[j]) " << endl
	  << "        * gEigenVectors[j *  gNVariables + i] " 
	  << "/ gSigmaValues[j];" << endl << endl << "  }" 
	  << endl << "}" << endl << endl;
  // 
  // Now: void p2x(Double_t *p, Double_t *x, Int_t nTest);
  // 
  outFile << "// " << endl << "// The " 
	  << (isMethod ? "method " : "function ")
	  << "  void " << prefix 
	  << "P2X(Double_t *p, Double_t *x, Int_t nTest)" 
	  << endl << "// " << endl;
  outFile << "void " << prefix 
	  << "P2X(Double_t *p, Double_t *x, Int_t nTest) {" << endl
	  << "  for (Int_t i = 0; i < gNVariables; i++) {" << endl
	  << "    x[i] = gMeanValues[i];" << endl
	  << "    for (Int_t j = 0; j < nTest; j++)" << endl
	  << "      x[i] = p[j] * gSigmaValues[i] " << endl
	  << "        * gEigenValues[j *  gNVariables + i];" << endl
	  << "  }" << endl << "}" << endl << endl;
  
  // EOF
  outFile << "// EOF for " << filename << endl;

  // Close the file 
  outFile.close();

  cout << "done" << endl;
}

//____________________________________________________________________
 void TPrincipal::MakeTridiagonal()
{
  // 
  /*

PRIVATE METHOD:
Tridiagonalise the covariance matrix according to the Householder method as described in Numerical Recipes in C section 11.2.

The basic idea is to perform orthogonal transformation, where each transformation eat away the off-diagonal elements, except the inner most.

   */
  // 

  // The comments in this algorithm are modified version of those in
  // "Numerical ...". Please refer to that book (web-page) for more on
  // the algorithm. 
  // Notice that we store the diagonal elements of the tridiagonal
  // matrix directly in fEigenVectors, hence no vector d is declared,
  // only a reference. Also, we may use the fEigenValues vector as
  // temporary storage space for the off-diagonal elements. 

  // Copy covariance matrix to temporary matrix, so that we leave
  // the covariance matrix intact;
  fEigenVectors = fCovarianceMatrix;
  TMatrixD& a   = fEigenVectors;
  TVectorD& d   = fEigenValues;
  TVectorD& e   = fOffDiagonal;
  Int_t&    n   = fNumberOfVariables;

  Double_t hh, g, f;
  Int_t i,j,k;
  
  for (i = n; i >= 2; i--) {
    Int_t    l     = i - 1;
    Double_t h     = 0;
    Double_t scale = 0;
    
    if (l > 1) {
      for (k = 1; k <= l; k++) 
	scale += TMath::Abs(a(i,k));
	
      if (scale == 0)
	// Skip transformation
	e(i) = a(i,l);

      else {
	for (k = 1; k <= l; k++) {
	  // Use scaled elements of a for transformation
	  a(i,k) /= scale;
	  // Calculate sigma in h
	  h += a(i,k) * a(i,k);
	}

	f      =  a(i,l);
	g      =  (f >= 0. ? -TMath::Sqrt(h) : TMath::Sqrt(h));
	e(i)   =  scale * g;
	h      -= f * g; // Now h is eq. (11.2.4) in "Numerical ..."
	a(i,l) =  f - g;
	f      = 0;

	for (j = 1; j <= l; j++) {
	  // Store the u/H in ith column of a;
	  a(j,i) = a(i,j) / h;
	  // Form element A dot u in g;
	  g = 0;
	  
	  for (k = 1; k <= j; k++) 
	    g += a(j,k) * a(i, k);
	 
	  for (k = j + 1; k <= l; k++) 
	    g += a(k,j) * a(i, k);

	  // Form element of vector p in temporarily unused element of
	  // e 
	  e(j) =  g / h;
	  f    += e(j) * a(i,j);
	}

	// Form K eq (11.2.11)
	hh = f / (h + h);

	// Form vector q and store in e overwriting p
	for (j = 1; j <= l; j++) {
	  f    = a(i,j);
	  e(j) = g = e(j) - hh * f;

	  for (k = 1; k <= j; k++) 
	    // Reduce a, eq (11.2.13)
	    a(j,k) -= (f * e(k) + g * a(i,k));
	}
      }
    }
    else
      e(i) = a(i,l);

    d(i) = h;
  }
  
  d(1) = 0;
  e(1) = 0;

  for (i = 1; i <= n; i++) {
    // Begin accumulation of transformation matrix
    Int_t l = i - 1;

    if (d(i)) {
      // This block is skipped if i = 1;
      for (j = 1; j <= l; j++) {
	g = 0;
	
	for (k = 1; k <= l; k++) 
	  // Use vector u/H stored in a to form P dot Q
	  g += a(i,k) * a(k,j);

	for (k = 1; k <= l; k++)
	  a(k,j) -= g * a(k,i);
      }
    }

    d(i)   = a(i,i);
    a(i,i) = 1;
    
    for (j = 1; j <= l; j++) {
      a(j,i) = a(i,j) = 0;
    }
  }

}

//____________________________________________________________________
 void TPrincipal::P2X(Double_t *p, Double_t *x, Int_t nTest)
{
  // Calculate x as a function of nTest of the most significant
  // principal components p, and return it in x.  
  // It's the users responsibility to make sure that both x and p are
  // of the right size (i.e., memory must be allocated for x). 

  for (Int_t i = 1; i <= fNumberOfVariables; i++){
    x[i-1] = fMeanValues(i);
    for (Int_t j = 1; j <= nTest; j++)
      x[i-1] += p[j-1] * fSigmas(i) * fEigenVectors(j,i);
  }

}

//____________________________________________________________________
 void TPrincipal::Print(Option_t *opt)
{
  // Print the statistics
  // Options are 
  //      M            Print mean values of original data 
  //      S            Print sigma values of original data 
  //      E            Print eigenvalues of covarinace matrix
  //      V            Print eigenvectors of covarinace matrix
  // Default is MSE

  Bool_t printV = kFALSE;
  Bool_t printM = kFALSE;
  Bool_t printS = kFALSE;
  Bool_t printE = kFALSE;
  
  Int_t len     = strlen(opt);
  for (Int_t i = 0; i < len; i++) {
    switch (opt[i]) {
    case 'V':
    case 'v':
      printV = kTRUE;
      break;
    case 'M':
    case 'm':
      printM = kTRUE;
      break;
    case 'S':
    case 's':
      printS = kTRUE;
      break;
    case 'E':
    case 'e':
      printE = kTRUE;
      break;
    default:
      Warning("Print", "Unknown option '%c'",opt[i]);
      break;
    }
  }
  
  if (printM||printS||printE) {
    cout << " Variable #  " << flush; 
    if (printM)
      cout << "| Mean Value " << flush;
    if (printS)
      cout << "|   Sigma    " << flush;
    if (printE)
      cout << "| Eigenvalue" << flush;
    cout << endl;

    cout << "-------------" << flush;
    if (printM)
      cout << "+------------" << flush;
    if (printS)
      cout << "+------------" << flush;
    if (printE)
      cout << "+------------" << flush;
    cout << endl;

    for (Int_t i = 1; i <= fNumberOfVariables; i++) {      
      cout << setw(12) << i << " " << flush;
      if (printM) 
	cout << "| " << setw(10) << setprecision(4) 
	     << fMeanValues(i) << " " << flush; 
      if (printS) 
	cout << "| " << setw(10) << setprecision(4) 
	     << fSigmas(i) << " " << flush; 
      if (printE) 
	cout << "| " << setw(10) << setprecision(4) 
	     << fEigenValues(i) << " " << flush; 
      cout << endl;
    }
    cout << endl;
  }
  
  if(printV) {
    for (Int_t i = 1; i <= fNumberOfVariables; i++) {
      cout << "Eigenvector # " << i << flush;
      TVectorD v(1,fNumberOfVariables);
      v = TMatrixDColumn(fEigenVectors,i);
      v.Print();
    }
  }
}

//____________________________________________________________________
 void TPrincipal::SumOfSquareResiduals(Double_t *x, Double_t *s)
{
  // PRIVATE METHOD: 
  // 
  /*

Calculates the sum of the square residuals, that is

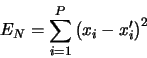
$\begin{displaymath} E_N = \sum_{i=1}^P \left(x_i - x^\prime_i\right)^2 \end{displaymath}$

where $x^\prime_i = \sum_{j=i}^N p_i e_{n_j}$ ,

is the $i^{\mbox{th}}$ component of the principal vector, corresponding to

, the original data; I.e., the square distance to the space spanned by

eigenvectors.

  */
  // 
  if (!x) 
    return;

  Double_t p[100];
  Double_t xp[100];

  X2P(x,p);
  for (Int_t i = fNumberOfVariables; i > 0; i--) {
    P2X(p,xp,i);
    for (Int_t j = 0; j < fNumberOfVariables; j++) {
      s[i] += (x[j] - xp[j])*(x[j] - xp[j]);
    }
  }
}

//____________________________________________________________________
 void TPrincipal::Test(Option_t *opt) 
{
  // Test the PCA, bye calculating the sum square of residuals 
  // (see method SumOfSquareResiduals), and display the histogram 
  MakeHistograms("pca","S");

  TH1 *pca_s = 0;
  if (fHistograms) pca_s = (TH1*)fHistograms->FindObject("pca_s");
  if (!pca_s) {
    Warning("Test", "Couldn't get histogram of square residuals"); 
    return;
  }
  
  pca_s->Draw();
}
      
//____________________________________________________________________
 void TPrincipal::X2P(Double_t *x, Double_t *p)
{
  // Calculate the principal components from the original data vector
  // x, and return it in p. 
  // It's the users responsibility to make sure that both x and p are
  // of the right size (i.e., memory must be allocated for p). 
  for (Int_t i = 1; i <= fNumberOfVariables; i++){
    p[i-1] = 0;
    for (Int_t j = 1; j <= fNumberOfVariables; j++)
      p[i-1] += (x[j-1] - fMeanValues(j)) * fEigenVectors(j,i) /
	fSigmas(j);
  }
  
}

ROOT page - Class index - Top of the page

This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.