TMath
class description - source file - inheritance tree
private:
static Double_t GamCf(Double_t a, Double_t x)
static Double_t GamSer(Double_t a, Double_t x)
public:
TMath TMath()
TMath TMath(TMath&)
void ~TMath()
static Short_t Abs(Short_t d)
static Int_t Abs(Int_t d)
static Long_t Abs(Long_t d)
static Float_t Abs(Float_t d)
static Double_t Abs(Double_t d)
static Double_t ACos(Double_t x)
static Double_t ACosH(Double_t)
static Double_t ASin(Double_t x)
static Double_t ASinH(Double_t)
static Double_t ATan(Double_t x)
static Double_t ATan2(Double_t y, Double_t x)
static Double_t ATanH(Double_t)
static Double_t BesselI(Int_t n, Double_t x)
static Double_t BesselI0(Double_t x)
static Double_t BesselI1(Double_t x)
static Double_t BesselK(Int_t n, Double_t x)
static Double_t BesselK0(Double_t x)
static Double_t BesselK1(Double_t x)
static Int_t BinarySearch(Int_t n, Short_t* array, Short_t value)
static Int_t BinarySearch(Int_t n, Short_t** array, Short_t value)
static Int_t BinarySearch(Int_t n, Int_t* array, Int_t value)
static Int_t BinarySearch(Int_t n, Int_t** array, Int_t value)
static Int_t BinarySearch(Int_t n, Float_t* array, Float_t value)
static Int_t BinarySearch(Int_t n, Float_t** array, Float_t value)
static Int_t BinarySearch(Int_t n, Double_t* array, Double_t value)
static Int_t BinarySearch(Int_t n, Double_t** array, Double_t value)
static Double_t Ceil(Double_t x)
static TClass* Class()
static Double_t Cos(Double_t x)
static Double_t CosH(Double_t x)
static Float_t* Cross(Float_t* v1, Float_t* v2, Float_t* out)
static Double_t* Cross(Double_t* v1, Double_t* v2, Double_t* out)
static Double_t E()
static Double_t Erf(Double_t x)
static Double_t Erfc(Double_t x)
static Bool_t Even(Long_t a)
static Double_t Exp(Double_t x)
static Double_t Floor(Double_t x)
static Double_t Gamma(Double_t z)
static Double_t Gamma(Double_t a, Double_t x)
static Double_t Gaus(Double_t x, Double_t mean = 0, Double_t sigma = 1)
static ULong_t Hash(const void* txt, Int_t ntxt)
static ULong_t Hash(const char* str)
static Double_t Hypot(Double_t x, Double_t y)
static Long_t Hypot(Long_t x, Long_t y)
virtual TClass* IsA() const
static Double_t KolmogorovProb(Double_t z)
static Double_t Landau(Double_t x, Double_t mean = 0, Double_t sigma = 1)
static Double_t LnGamma(Double_t z)
static Int_t LocMax(Int_t n, Short_t* a)
static Int_t LocMax(Int_t n, Int_t* a)
static Int_t LocMax(Int_t n, Float_t* a)
static Int_t LocMax(Int_t n, Double_t* a)
static Int_t LocMin(Int_t n, Short_t* a)
static Int_t LocMin(Int_t n, Int_t* a)
static Int_t LocMin(Int_t n, Float_t* a)
static Int_t LocMin(Int_t n, Double_t* a)
static Double_t Log(Double_t x)
static Double_t Log10(Double_t x)
static Double_t Log2(Double_t x)
static Short_t Max(Short_t a, Short_t b)
static UShort_t Max(UShort_t a, UShort_t b)
static Int_t Max(Int_t a, Int_t b)
static UInt_t Max(UInt_t a, UInt_t b)
static Long_t Max(Long_t a, Long_t b)
static ULong_t Max(ULong_t a, ULong_t b)
static Float_t Max(Float_t a, Float_t b)
static Double_t Max(Double_t a, Double_t b)
static Short_t Min(Short_t a, Short_t b)
static UShort_t Min(UShort_t a, UShort_t b)
static Int_t Min(Int_t a, Int_t b)
static UInt_t Min(UInt_t a, UInt_t b)
static Long_t Min(Long_t a, Long_t b)
static ULong_t Min(ULong_t a, ULong_t b)
static Float_t Min(Float_t a, Float_t b)
static Double_t Min(Double_t a, Double_t b)
static Long_t NextPrime(Long_t x)
static Int_t Nint(Float_t x)
static Int_t Nint(Double_t x)
static Float_t* Normal2Plane(Float_t* v1, Float_t* v2, Float_t* v3, Float_t* normal)
static Double_t* Normal2Plane(Double_t* v1, Double_t* v2, Double_t* v3, Double_t* normal)
static Float_t Normalize(Float_t* v)
static Double_t Normalize(Double_t* v)
static Float_t NormCross(Float_t* v1, Float_t* v2, Float_t* out)
static Double_t NormCross(Double_t* v1, Double_t* v2, Double_t* out)
static Bool_t Odd(Long_t a)
static Double_t Pi()
static Double_t Power(Double_t x, Double_t y)
static Double_t Prob(Double_t chi2, Int_t ndf)
static Short_t Range(Short_t lb, Short_t ub, Short_t x)
static Int_t Range(Int_t lb, Int_t ub, Int_t x)
static Long_t Range(Long_t lb, Long_t ub, Long_t x)
static ULong_t Range(ULong_t lb, ULong_t ub, ULong_t x)
static Double_t Range(Double_t lb, Double_t ub, Double_t x)
virtual void ShowMembers(TMemberInspector& insp, char* parent)
static Short_t Sign(Short_t a, Short_t b)
static Int_t Sign(Int_t a, Int_t b)
static Long_t Sign(Long_t a, Long_t b)
static Float_t Sign(Float_t a, Float_t b)
static Double_t Sign(Double_t a, Double_t b)
static Double_t Sin(Double_t x)
static Double_t SinH(Double_t x)
static void Sort(Int_t n, Short_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, Int_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, Float_t* a, Int_t* index, Bool_t down = kTRUE)
static void Sort(Int_t n, Double_t* a, Int_t* index, Bool_t down = kTRUE)
static Double_t Sqrt(Double_t x)
static Long_t Sqrt(Long_t x)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
static Double_t Tan(Double_t x)
static Double_t TanH(Double_t x)
TMath
Encapsulate math routines (i.e. provide a kind of namespace).
For the time being avoid templates.
Long_t Sqrt(Long_t x)
Double_t Hypot(Double_t x, Double_t y)
Double_t ASinH(Double_t x)
Double_t ACosH(Double_t x)
Double_t ATanH(Double_t x)
Double_t Ceil(Double_t x)
Double_t Floor(Double_t x)
Double_t Log2(Double_t x)
Long_t NextPrime(Long_t x)
Return next prime number after x, unless x is a prime in which case
x is returned.
Int_t Nint(Float_t x)
Round to nearest integer. Rounds half integers to the nearest
even integer.
Int_t Nint(Double_t x)
Round to nearest integer. Rounds half integers to the nearest
even integer.
Float_t* Cross(Float_t v1[3],Float_t v2[3],Float_t out[3])
Calculate the Cross Product of two vectors
out = [v1 x v2]
Double_t* Cross(Double_t v1[3],Double_t v2[3],Double_t out[3])
Calculate the Cross Product of two vectors
out = [v1 x v2]
Double_t Erf(Double_t x)
Computation of the error function erf(x).
--- NvE 14-nov-1998 UU-SAP Utrecht
Double_t Erfc(Double_t x)
Computation of the complementary error function erfc(x).
The algorithm is based on a Chebyshev fit as denoted in
Numerical Recipes 2nd ed. on p. 214 (W.H.Press et al.).
The fractional error is always less than 1.2e-7.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Gamma(Double_t z)
Computation of gamma(z) for all z>0.
The algorithm is based on the article by C.Lanczos [1] as denoted in
Numerical Recipes 2nd ed. on p. 207 (W.H.Press et al.).
[1] C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Gamma(Double_t a,Double_t x)
Computation of the incomplete gamma function P(a,x)
The algorithm is based on the formulas and code as denoted in
Numerical Recipes 2nd ed. on p. 210-212 (W.H.Press et al.).
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t GamCf(Double_t a,Double_t x)
Computation of the incomplete gamma function P(a,x)
via its continued fraction representation.
The algorithm is based on the formulas and code as denoted in
Numerical Recipes 2nd ed. on p. 210-212 (W.H.Press et al.).
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t GamSer(Double_t a,Double_t x)
Computation of the incomplete gamma function P(a,x)
via its series representation.
The algorithm is based on the formulas and code as denoted in
Numerical Recipes 2nd ed. on p. 210-212 (W.H.Press et al.).
--- Nve 14-nov-1998 UU-SAP Utrecht
Double_t Gaus(Double_t x, Double_t mean, Double_t sigma)
Calculate a gaussian function with mean and sigma
Double_t Landau(Double_t x, Double_t mean, Double_t sigma)
The LANDAU function with mean and sigma.
This function has been adapted from the CERNLIB routine G110 denlan.
Double_t LnGamma(Double_t z)
Computation of ln[gamma(z)] for all z>0.
The algorithm is based on the article by C.Lanczos [1] as denoted in
Numerical Recipes 2nd ed. on p. 207 (W.H.Press et al.).
[1] C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
The accuracy of the result is better than 2e-10.
--- Nve 14-nov-1998 UU-SAP Utrecht
Float_t Normalize(Float_t v[3])
Normalize a vector v in place
Return:
The norm of the original vector
Double_t Normalize(Double_t v[3])
Normalize a vector v in place
Return:
The norm of the original vector
Float_t* Normal2Plane(Float_t p1[3],Float_t p2[3],Float_t p3[3], Float_t normal[3])
Calculate a normal vector of a plane
Input:
Float_t *p1,*p2,*p3 - 3 3D points belonged the plane to define it.
Return:
Pointer to 3D normal vector (normalized)
Double_t* Normal2Plane(Double_t p1[3],Double_t p2[3],Double_t p3[3], Double_t normal[3])
Calculate a normal vector of a plane
Input:
Float_t *p1,*p2,*p3 - 3 3D points belonged the plane to define it.
Return:
Pointer to 3D normal vector (normalized)
Double_t Prob(Double_t chi2,Int_t ndf)
Computation of the probability for a certain Chi-squared (chi2)
and number of degrees of freedom (ndf).
Calculations are based on the incomplete gamma function P(a,x),
where a=ndf/2 and x=chi2/2.
P(a,x) represents the probability that the observed Chi-squared
for a correct model should be less than the value chi2.
The returned probability corresponds to 1-P(a,x),
which denotes the probability that an observed Chi-squared exceeds
the value chi2 by chance, even for a correct model.
--- NvE 14-nov-1998 UU-SAP Utrecht
Double_t KolmogorovProb(Double_t z)
Calculates the Kolmogorov distribution function,
/*
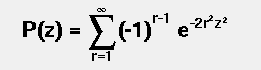 */
which gives the probability that Kolmogorov's test statistic will exceed
the value z assuming the null hypothesis. This gives a very powerful
test for comparing two one-dimensional distributions.
see, for example, Eadie et al, "statistocal Methods in Experimental
Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where:
z = dn*sqrt(n), and
dn is the maximum deviation between a hypothetical distribution
function and an experimental distribution with
n events
NOTE: To compare two experimental distributions with m and n events,
use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application.
Probabilities less than 10^-15 are returned as zero.
However, remember that the formula is only valid for "large" n.
Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB
*/
which gives the probability that Kolmogorov's test statistic will exceed
the value z assuming the null hypothesis. This gives a very powerful
test for comparing two one-dimensional distributions.
see, for example, Eadie et al, "statistocal Methods in Experimental
Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where:
z = dn*sqrt(n), and
dn is the maximum deviation between a hypothetical distribution
function and an experimental distribution with
n events
NOTE: To compare two experimental distributions with m and n events,
use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application.
Probabilities less than 10^-15 are returned as zero.
However, remember that the formula is only valid for "large" n.
Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB
Int_t LocMin(Int_t n, Short_t *a)
Return index of array with the minimum element
If more than one element is minimum returns first found
Int_t LocMin(Int_t n, Int_t *a)
Return index of array with the minimum element
If more than one element is minimum returns first found
Int_t LocMin(Int_t n, Float_t *a)
Return index of array with the minimum element
If more than one element is minimum returns first found
Int_t LocMin(Int_t n, Double_t *a)
Return index of array with the minimum element
If more than one element is minimum returns first found
Int_t LocMax(Int_t n, Short_t *a)
Return index of array with the maximum element
If more than one element is maximum returns first found
Int_t LocMax(Int_t n, Int_t *a)
Return index of array with the maximum element
If more than one element is maximum returns first found
Int_t LocMax(Int_t n, Float_t *a)
Return index of array with the maximum element
If more than one element is maximum returns first found
Int_t LocMax(Int_t n, Double_t *a)
Return index of array with the maximum element
If more than one element is maximum returns first found
Int_t BinarySearch(Int_t n, Short_t *array, Short_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Short_t **array, Short_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Int_t *array, Int_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Int_t **array, Int_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Float_t *array, Float_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Float_t **array, Float_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Double_t *array, Double_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
Int_t BinarySearch(Int_t n, Double_t **array, Double_t value)
Binary search in an array of n values to locate value
Array is supposed to be sorted prior to this call.
If match is found, function returns position of element.
If no match found, function gives nearest element smaller than value.
void Sort(Int_t n1, Short_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Short_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, Int_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Int_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, Float_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Float_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
void Sort(Int_t n1, Double_t *a, Int_t *index, Bool_t down)
Sort the n1 elements of the Double_t array a.
In output the array index contains the indices of the sorted array.
If down is false sort in increasing order (default is decreasing order).
This is a translation of the CERNLIB routine sortzv (M101)
based on the quicksort algorithm.
NOTE that the array index must be created with a length >= n1
before calling this function.
ULong_t Hash(const void *txt, Int_t ntxt)
Calculates hash index from any char string
based on precalculated table of 256 specially selected
random numbers.
For string: i = TMath::Hash(string,nstring);
For int: i = TMath::Hash(&intword,sizeof(int));
For pointer: i = TMath::Hash(&pointer,sizeof(void*));
Limitation: for ntxt>256 calculates hash only from first 256 bytes
V.Perev
ULong_t Hash(const char *txt)
Double_t BesselI0(Double_t x)
Computation of the modified Bessel function I_0(x) for any real x.
The algorithm is based on the article by Abramowitz and Stegun [1]
as denoted in Numerical Recipes 2nd ed. on p. 230 (W.H.Press et al.).
[1] M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK0(Double_t x)
Computation of the modified Bessel function K_0(x) for positive real x.
The algorithm is based on the article by Abramowitz and Stegun [1]
as denoted in Numerical Recipes 2nd ed. on p. 230 (W.H.Press et al.).
[1] M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselI1(Double_t x)
Computation of the modified Bessel function I_1(x) for any real x.
The algorithm is based on the article by Abramowitz and Stegun [1]
as denoted in Numerical Recipes 2nd ed. on p. 230 (W.H.Press et al.).
[1] M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK1(Double_t x)
Computation of the modified Bessel function K_1(x) for positive real x.
The algorithm is based on the article by Abramowitz and Stegun [1]
as denoted in Numerical Recipes 2nd ed. on p. 230 (W.H.Press et al.).
[1] M.Abramowitz and I.A.Stegun, Handbook of Mathematical Functions,
Applied Mathematics Series vol. 55 (1964), Washington.
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselK(Int_t n,Double_t x)
Computation of the Integer Order Modified Bessel function K_n(x)
for n=0,1,2,... and positive real x.
The algorithm uses the recurrence relation
K_n+1(x) = (2n/x)*K_n(x) + K_n-1(x)
as denoted in Numerical Recipes 2nd ed. on p. 232 (W.H.Press et al.).
--- NvE 12-mar-2000 UU-SAP Utrecht
Double_t BesselI(Int_t n,Double_t x)
Computation of the Integer Order Modified Bessel function I_n(x)
for n=0,1,2,... and any real x.
The algorithm uses the recurrence relation
I_n+1(x) = (-2n/x)*I_n(x) + I_n-1(x)
as denoted in Numerical Recipes 2nd ed. on p. 232 (W.H.Press et al.).
--- NvE 12-mar-2000 UU-SAP Utrecht
Inline Functions
Double_t Pi()
Double_t E()
Double_t Sin(Double_t x)
Double_t Cos(Double_t x)
Double_t Tan(Double_t x)
Double_t SinH(Double_t x)
Double_t CosH(Double_t x)
Double_t TanH(Double_t x)
Double_t ASin(Double_t x)
Double_t ACos(Double_t x)
Double_t ATan(Double_t x)
Double_t ATan2(Double_t y, Double_t x)
Double_t Exp(Double_t x)
Double_t Power(Double_t x, Double_t y)
Double_t Log(Double_t x)
Double_t Log10(Double_t x)
Long_t Sqrt(Long_t x)
Long_t Hypot(Long_t x, Long_t y)
Short_t Abs(Short_t d)
Int_t Abs(Int_t d)
Long_t Abs(Long_t d)
Float_t Abs(Float_t d)
Double_t Abs(Double_t d)
Bool_t Even(Long_t a)
Bool_t Odd(Long_t a)
Short_t Sign(Short_t a, Short_t b)
Int_t Sign(Int_t a, Int_t b)
Long_t Sign(Long_t a, Long_t b)
Float_t Sign(Float_t a, Float_t b)
Double_t Sign(Double_t a, Double_t b)
Short_t Min(Short_t a, Short_t b)
UShort_t Min(UShort_t a, UShort_t b)
Int_t Min(Int_t a, Int_t b)
UInt_t Min(UInt_t a, UInt_t b)
Long_t Min(Long_t a, Long_t b)
ULong_t Min(ULong_t a, ULong_t b)
Float_t Min(Float_t a, Float_t b)
Double_t Min(Double_t a, Double_t b)
Short_t Max(Short_t a, Short_t b)
UShort_t Max(UShort_t a, UShort_t b)
Int_t Max(Int_t a, Int_t b)
UInt_t Max(UInt_t a, UInt_t b)
Long_t Max(Long_t a, Long_t b)
ULong_t Max(ULong_t a, ULong_t b)
Float_t Max(Float_t a, Float_t b)
Double_t Max(Double_t a, Double_t b)
Short_t Range(Short_t lb, Short_t ub, Short_t x)
Int_t Range(Int_t lb, Int_t ub, Int_t x)
Long_t Range(Long_t lb, Long_t ub, Long_t x)
ULong_t Range(ULong_t lb, ULong_t ub, ULong_t x)
Double_t Range(Double_t lb, Double_t ub, Double_t x)
Float_t NormCross(Float_t* v1, Float_t* v2, Float_t* out)
Double_t NormCross(Double_t* v1, Double_t* v2, Double_t* out)
TClass* Class()
TClass* IsA() const
void ShowMembers(TMemberInspector& insp, char* parent)
void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
TMath TMath()
TMath TMath(TMath&)
void ~TMath()
Author: Fons Rademakers 29/07/95
Last update: root/base:$Name: $:$Id: TMath.cxx,v 1.7 2000/11/30 10:52:13 rdm Exp $
Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
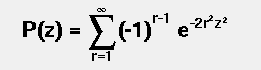 */
which gives the probability that Kolmogorov's test statistic will exceed
the value z assuming the null hypothesis. This gives a very powerful
test for comparing two one-dimensional distributions.
see, for example, Eadie et al, "statistocal Methods in Experimental
Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where:
z = dn*sqrt(n), and
dn is the maximum deviation between a hypothetical distribution
function and an experimental distribution with
n events
NOTE: To compare two experimental distributions with m and n events,
use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application.
Probabilities less than 10^-15 are returned as zero.
However, remember that the formula is only valid for "large" n.
Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB
*/
which gives the probability that Kolmogorov's test statistic will exceed
the value z assuming the null hypothesis. This gives a very powerful
test for comparing two one-dimensional distributions.
see, for example, Eadie et al, "statistocal Methods in Experimental
Physics', pp 269-270).
This function returns the confidence level for the null hypothesis, where:
z = dn*sqrt(n), and
dn is the maximum deviation between a hypothetical distribution
function and an experimental distribution with
n events
NOTE: To compare two experimental distributions with m and n events,
use z = sqrt(m*n/(m+n))*dn
Accuracy: The function is far too accurate for any imaginable application.
Probabilities less than 10^-15 are returned as zero.
However, remember that the formula is only valid for "large" n.
Theta function inversion formula is used for z <= 1
This function was translated by Rene Brun from PROBKL in CERNLIB